Минором k-го порядка произвольной матрицы А называется определитель составленный из элементов матрицы, расположенных на пересечении каких-либо k-строк и k-столбцов.
В матрице 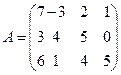 можно указать, например такие миноры:
можно указать, например такие миноры:
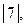
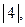
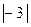 - 1-го порядка
- 1-го порядка
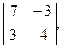
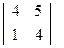 - 2-го порядка
- 2-го порядка
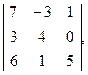
 - 3-го порядка
- 3-го порядка
Рангом матрицы А называется наибольший из порядков её миноров, не равных нулю. Обозначается 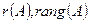 .
.
Методы вычисления ранга матрицы:
а) метод окаймляющих миноров
Метод окаймляющих миноров нахождения ранга матрицы А состоит в следующем:
1) необходимо найти какой-нибудь минор М 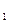 первого порядка, отличный от нуля.
первого порядка, отличный от нуля.
Если такого минора нет, то матрица А нулевая и 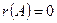 ;
;
2) Вычислить миноры 2-го порядка, содержащие М 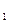 (окаймляющие М
(окаймляющие М 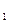 ) до тех пор, пока не найдется минор М
) до тех пор, пока не найдется минор М 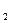 , отличный от нуля. Если такого минора нет, то
, отличный от нуля. Если такого минора нет, то 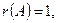
если есть, то 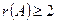 . и т.д.
. и т.д.
3) Вычислить (если он существует) минор k-го порядка окаймляющие миноры 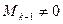 . Если таких миноров нет, или они все равны нулю, то
. Если таких миноров нет, или они все равны нулю, то 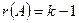 ; если хотя бы один такой минор
; если хотя бы один такой минор  , то
, то 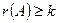 и процесс продолжается.
и процесс продолжается.
Пример. Найти ранг матрицы методом окаймляющих миноров
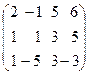 .
.
Решение.
Так как у матрицы А есть ненулевые элементы, то
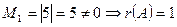 или
или 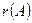 >1
>1
Найдём какой-либо ненулевой минор 2-го порядка (если он существует)
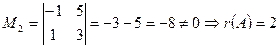 или
или 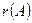 >2
>2
Вычислим миноры 3-го порядка, окаймляющие 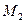
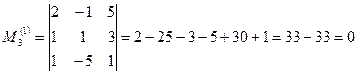
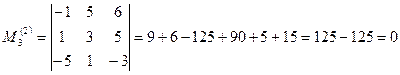
Все миноры 3-го порядка, окаймляющие 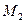 , равны нулю, следовательно
, равны нулю, следовательно 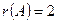 .
.
 2015-01-21
2015-01-21 555
555








