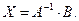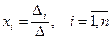Основные понятия. Пусть задана система из m линейных уравнений с n неизвестными

Пусть задана система из m линейных уравнений с n неизвестными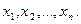

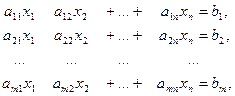
где числа 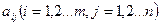называется коэффициентами системы, а числа 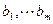свободными членами.

Если система имеет хотя бы одно решение, она называется совместной; система, не имеющая, ни одного решения называется несовместной.

Система называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы линейных уравнений с одинаковым числом неизвестных называются эквивалентными, если множество всех решений этих систем совпадают.

Если 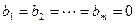, то система называется однородной, в противном случае она называется неоднородной.

Пусть система из n линейных уравнений с n неизвестными записана в матричной форме

,

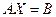где 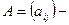матрица коэффициентов системы ,

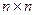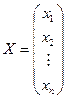- столбец неизвестных,

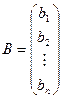- столбец свободных членов.

Матрица (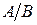) = 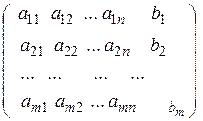, называется расширенной матрицей системы.

4.2. Решение систем линейных уравнений с помощью обратной матрицы (матричный способ). Формулы Крамера

Пусть дана система n линейных уравнений с n неизвестными

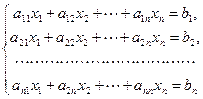
или в матричной форме .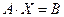

Основная матрица А такой системы квадратная. Определитель этой матрицы

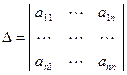
называется определителем системы. Если определитель системы отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае .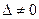

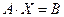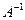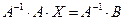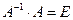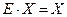Умножив обе части уравнения слева на матрицу , получим . Поскольку и , то

(4.1)

Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.

Матричное равенство (4.1) запишем в виде

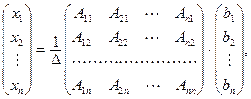
то есть

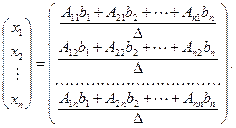
Отсюда следует, что

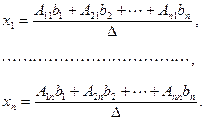
Но 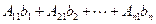есть разложение определителя

по элементам первого столбца. Определитель 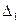получается из определителя 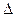путем замены первого столбца коэффициентов столбцом из свободных членов.

Итак, .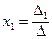

Аналогично: 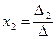, где 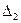получен из 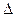путем замены второго столбца коэффициентов столбцом из свободных членов; .

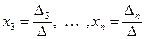Формулы

называются формулами Крамера.

Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом (4.1) либо по формулам Крамера (4.2).

Пример. Найти решения линейной системы уравнения использую обратную матрицу и формулы Крамера

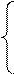
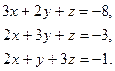
Решение.

Найдем определитель матрицы системы:

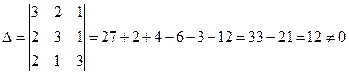система имеет единственное решение.

Найдем :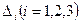

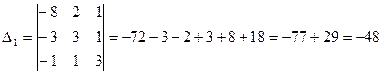
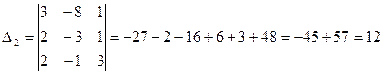
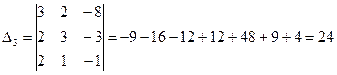
Отсюда получим решение системы уравнений (по формулам Крамера)

, , .

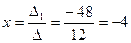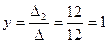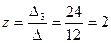Ответ: (-4;1;2).

Решим данную систему, используя обратную матрицу.

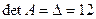, найдем 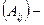матрицу алгебраических дополнений:

;

; ;

;

,

= .

,

,

.

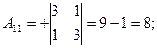
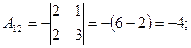
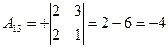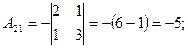
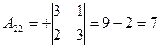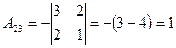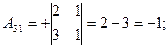
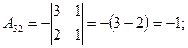
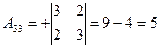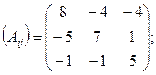
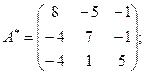
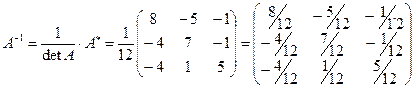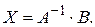
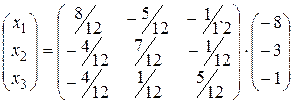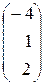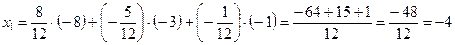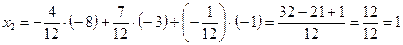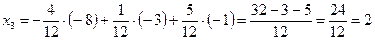Ответ: (-4;1;2).