Вариант 1
1. Определить, есть ли тупой угол среди внутренних углов треугольника АВС, если А(4,-1,4), В(0,7,-4) и С(3,1,-2).
2. Даны точки А(-1,5,-10), В(5, -7,8), С (2,2,-7), D (5,-4,2). Проверить, что векторы АВ и СD коллинеарные, установить какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
3. Векторы 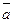 и
и 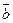 взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор 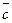 образует с ними углы, равные
образует с ними углы, равные 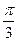
 . Зная, что
. Зная, что 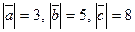 , вычислить
, вычислить 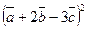 .
.
4. Даны вершины треугольника А(1,-1,2), В(5,-6,2) и С(1,3,-1). Вычислить длину его высоты, опущенной из вершины В на сторону АС.
5. Проверить компланарность векторов 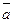 (2,-1,3),
(2,-1,3), 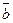 (1,0,-1),
(1,0,-1), 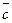 (2,4,1).
(2,4,1).
6. На плоскости даны два вектора 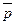 (1, -3) и
(1, -3) и 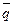 (2, -5). Найти разложение
(2, -5). Найти разложение 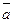 (6,1) по базису
(6,1) по базису 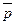 ,
, 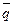 .
.
Вариант 2
1. Доказать, что внутренние углы треугольника АВС, где А(3,-2,5), В(-2,1,-3), С(5,1,-1), острые.
2. Даны точки А(1,-1,4), В(-2, 11,-2), С (4,0,-7), D (5,-4,-5). Проверить, что векторы АВ и СD коллинеарные, установить какой из них длиннее другого и во сколько раз, как они направлены – в одну или в противоположные стороны.
3. Векторы 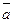 и
и 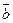 взаимно перпендикулярны, вектор
взаимно перпендикулярны, вектор 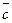 образует с ними углы, равные
образует с ними углы, равные 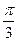
 . Зная, что
. Зная, что 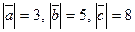 , вычислить
, вычислить 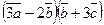 .
.
4. Даны вершины треугольника А(1,2,0), В(3,0,-3) и С(5,2,6). Вычислить длину его высоты, опущенной из вершины А на сторону ВС.
5. Проверить компланарность векторов 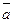 (3,-1,4),
(3,-1,4), 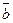 (1,1,2),
(1,1,2), 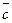 (0,1,-3).
(0,1,-3).
6. На плоскости даны два вектора 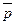 (2, -4) и
(2, -4) и 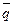 (3, 4). Найти разложение
(3, 4). Найти разложение 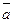 (2,5) по базису
(2,5) по базису 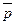 ,
, 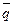 .
.
 2015-01-21
2015-01-21 1516
1516








