Основные формулы. Среднее линейное отклонение (

Размах вариации ():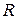

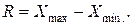
(1.1)

Среднее линейное отклонение ():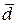

а) для несгруппированных данных:

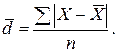
(1.2)

б) для сгруппированных данных:

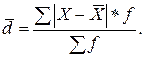
(1.3)

Дисперсия (s²):

а) простая дисперсия для несгруппированных данных:

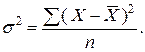
(1.4)

б) взвешенная дисперсия для вариационного ряда:

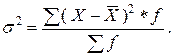
(1.5)

Упрощенные методы расчета дисперсии:

1. Метод электронно-вычислительного способа расчета:

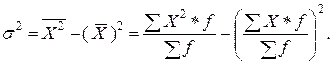
(1.6)

2. По «способу моментов»:

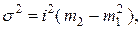
(1.7)

где m₂ – момент второго порядка, определяемый по формуле:

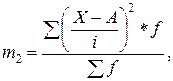
(1.8)

где m₁ – момент первого порядка, определяемый по формуле (4.10).

Дисперсия альтернативного признака ():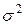

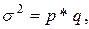
(1.9)

где p – доля единиц, обладающих альтернативным признаком;

q – доля единиц, не обладающих альтернативным признаком(q = 1 - p).

Среднее квадратическое отклонение (s):

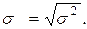
(1.10)

Правило сложения дисперсий:

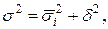
(1.11)

где s² – общая дисперсия;

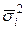- средняя из внутригрупповых дисперсий;

d² – дисперсия групповых средних (межгрупповая) дисперсия.

Средняя из внутригрупповых дисперсий:

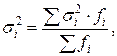
(1.12)

где 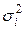- групповые дисперсии.

Внутригрупповые дисперсии:

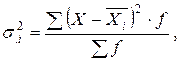
(1.13)

где 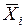- групповые средние;

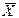- общая средняя.

Межгрупповая дисперсия:

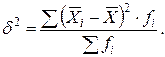
(1.14)

Коэффициент вариации ():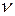

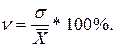
(1.15)

Коэффициент детерминации ():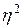

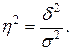
(1.16)

Эмпирическое корреляционное отношение ():

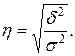
(1.17)