Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердого тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.
Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраняются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Реальные тела под действием внешних сил, как правило, испытывают упругие и пластические деформации пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать лишь упругие деформации, что мы и будем делать.
В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходящим деформациям растяжения или сжатия и сдвига.
Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы 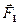 и
и 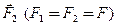 , в результате чего длина стержня меняется на величину
, в результате чего длина стержня меняется на величину 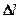 . Естественно, что при растяжении
. Естественно, что при растяжении 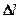 положительно, а при сжатии — отрицательно.
положительно, а при сжатии — отрицательно.

Сила, действующая на единицу площади поперечного сечения, называется напряжением:
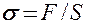 (21.1)
(21.1)
Если сила направлена по нормали к поверхности, напряжение называется нормальным, если же по касательной к поверхности — тангенциальным.
Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация. Так, относительное изменение длины стержня (продольная деформация)

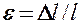 , (21.2)
, (21.2)
относительное поперечное растяжение (сжатие)
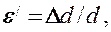
где d — диаметр стержня.
Деформации 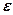 и
и  всегда имеют разные знаки. Из опыта вытекает их взаимосвязь:
всегда имеют разные знаки. Из опыта вытекает их взаимосвязь:
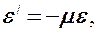
где 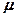 — положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона (С. Пуассон (1781—1840) — французский ученый).
— положительный коэффициент, зависящий от свойств материала, называемый коэффициентом Пуассона (С. Пуассон (1781—1840) — французский ученый).
Английский физик Р. Гук (1635— 1703) экспериментально установил, что для малых деформаций относительное удлинение 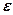 и напряжение
и напряжение 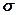 прямо пропорциональны друг другу:
прямо пропорциональны друг другу:
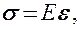 (21.3)
(21.3)
где коэффициент пропорциональности Е называется модулем Юнга (Т. Юнг (1773—1829) — английский ученый).
Из выражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (21.2), (21.3) и (21.1) вытекает, что
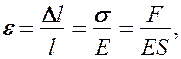
или
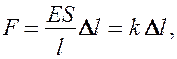 (21.4)
(21.4)
где k — коэффициент упругости. Выражение (21.4) также задает закон Гука, согласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.
Деформации твердых тел подчиняются закону Гука лишь в очень узких пределах (до предела пропорциональности 
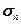 ). При дальнейшем увеличении напряжения зависимость
). При дальнейшем увеличении напряжения зависимость 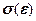 уже нелинейна, хотя деформация еще упругая вплоть до предела упругости (
уже нелинейна, хотя деформация еще упругая вплоть до предела упругости (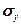 ) и остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации, т.е. тело в первоначальное состояние после прекращения действия силы не возвращается. Напряжение, при котором появляется заметная остаточная деформация (» 0,2 %), называется пределом текучести (
) и остаточные деформации не возникают. За пределом упругости в теле возникают остаточные деформации, т.е. тело в первоначальное состояние после прекращения действия силы не возвращается. Напряжение, при котором появляется заметная остаточная деформация (» 0,2 %), называется пределом текучести (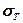 ). При этом деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, а для которых область текучести практически отсутствует — хрупкими. При дальнейшем растяжении тела происходит его разрушение. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности (
). При этом деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или областью пластических деформаций). Материалы, для которых область текучести значительна, называются вязкими, а для которых область текучести практически отсутствует — хрупкими. При дальнейшем растяжении тела происходит его разрушение. Максимальное напряжение, возникающее в теле до разрушения, называется пределом прочности (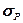 ).
).
Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.
Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, которая равна работе, совершаемой внешними силами при деформации:
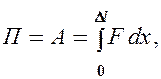
где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0до 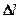 . Согласно закону Гука (21.4),
. Согласно закону Гука (21.4), 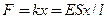 . Поэтому
. Поэтому

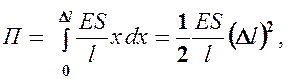
т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадрату деформации 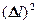 .
.
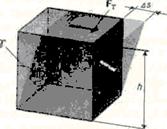
Рис. 36
Деформацию сдвига проще всего осуществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу 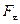 (рис.36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы
(рис.36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига определяется из формулы
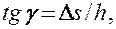
где 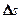 — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых углов
— абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых углов 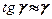 ).
).
Контрольные вопросы
· Что такое момент инерции тела?
· Какова роль момента инерции во вращательном движении? Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси, и как ее вывести?
· Что называется моментом силы относительно неподвижной точки? относительно неподвижной оси? Как определяется направление момента силы?
· Выведите и сформулируйте уравнение динамики вращательного движения твердого тела. Что такое момент импульса материальной точки? твердого тела? Как определяется направление момента импульса?
· В чем заключается физическая сущность закона сохранения момента импульса? В каких системах он выполняется? Приведите примеры.
· Каким свойством симметрии пространства обусловливается справедливость закона сохранения момента импульса?
· Сопоставьте основные уравнения динамики поступательного и вращательного движений, прокомментировав их аналогию.
· Что такое свободные оси (главные оси инерции)? Какие из них являются устойчивыми? Что такое гироскоп? Каковы его основные свойства?
· Сформулируйте закон Гука. Когда он справедлив?
· Что такое пределы пропорциональности, упругости и прочности? Каков физический смысл модуля Юнга?
Задачи
4.1. С одного уровня наклонной плоскости одновременно начинают скатываться без скольжения сплошные цилиндр и шар одинаковых масс и одинаковых радиусов. Определить: 1) отношение скоростей цилиндра и шара на данном уровне; 2) их отношение в данный момент времени. [1) 14/15; 2) 14/15 ]
4.2. К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касательная сила F =100 Н. При вращении диска на него действует момент сил трения М=2 Н м. Определить массу т диска, если известно, что его угловое ускорение 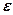 постоянно и равно 12 рад/с2 [32 кг]
постоянно и равно 12 рад/с2 [32 кг]
4.3. Через неподвижный блок в виде однородного сплошного цилиндра массой m = 1 кг перекинута невесомая нить, к концам которой прикреплены тела массами 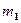 = 1 кг и
= 1 кг и 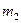 = 2 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) отношения
= 2 кг. Пренебрегая трением в оси блока, определить: 1) ускорение грузов; 2) отношения 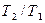 сил натяжения нити. [1) 2,8 м/с2; 2) 1,11 ]
сил натяжения нити. [1) 2,8 м/с2; 2) 1,11 ]
4.4. Скорость вращения колеса, момент инерции которого 2 кг м2, вращающегося при торможении равнозамедленно, за время t =1 мин уменьшилась от 300 об/мин до 180 об/мин. Определить: 1) угловое ускорение 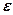 колеса; 2) момент М силы торможения; 3) работу силы торможения. [1) 0,21 рад/с2; 2) 0,42 Н м; 3) 630 Дж]
колеса; 2) момент М силы торможения; 3) работу силы торможения. [1) 0,21 рад/с2; 2) 0,42 Н м; 3) 630 Дж]
4.5. Человек массой m = 80 кг, стоящий на краю горизонтальной платформы массой M = 100 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой 10 об/мин, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точечной массой, определить, с какой частотой будет тогда вращаться платформа. [26 об/мин ]
4.6. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа 621 Дж. Длина стержня 2 м, площадь поперечного сечения 1 мм2, модуль Юнга для алюминия Е = 69 ГПа. [ 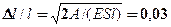 ]
]
 2015-01-21
2015-01-21 4659
4659