При сравнении законов вращательного и поступательного движений просматривается аналогия между ними, только при вращательном движении вместо силы «выступает» ее момент, а роль массы играет момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.
Моментом импульса (количества движения) материальной точки А относительно неподвижной точки О называется физическая величина, определяемая векторным произведением:

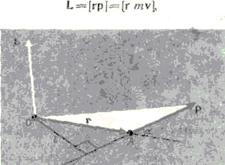
Рис. 28
где 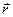 — радиус-вектор, проведенный из точки О в точку A;
— радиус-вектор, проведенный из точки О в точку A; 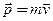 — импульс материальной точки (рис.28);
— импульс материальной точки (рис.28); 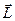 — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от
— псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от 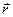 к
к 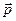 .
.
Модуль вектора момента импульса
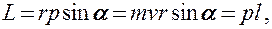
где 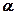 — угол между векторами
— угол между векторами 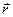 и
и 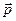 ,
, 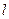 — плечо вектора
— плечо вектора 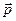 относительно точки О.
относительно точки О.
Моментом импульса относительно неподвижной оси z называется скалярная величина 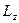 , равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса
, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О данной оси. Значение момента импульса 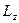 не зависит от положения точки О на оси z.
не зависит от положения точки О на оси z.
При вращении абсолютно твердого тела вокруг неподвижной оси z каждая отдельная точка тела движется по окружности постоянного радиуса 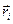 , с некоторой скоростью
, с некоторой скоростью 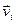 . Скорость
. Скорость 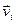 и импульс
и импульс 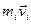 перпендикулярны этому радиусу, т.е. радиус является плечом вектора
перпендикулярны этому радиусу, т.е. радиус является плечом вектора 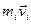 . Поэтому можем записать, что момент импульса отдельной частицы
. Поэтому можем записать, что момент импульса отдельной частицы
 (19.1)
(19.1)
и направлен по оси в сторону, определяемую правилом правого винта.
Момент импульса твердого тела относительно оси есть сумма моментов импульса отдельных его частиц:
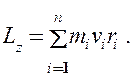
Используя формулу (17.1) 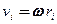 , получим
, получим
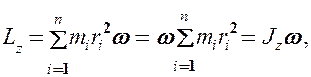
т.е.
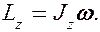 (19.2)
(19.2)
Таким образом, момент импульса твердого тела относительно оси равен произведению момента инерции тела относительно той же оси на угловую скорость.
Продифференцируем уравнение (19.2) по времени:
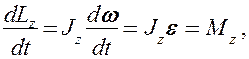
т. е.
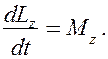
Это выражение — еще одна форма уравнения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.
Можно показать, что имеет место векторное равенство
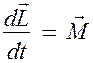 . (19.3)
. (19.3)
В замкнутой системе момент внешних сил  и
и 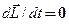 , откуда
, откуда
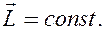 (19.4)
(19.4)
Выражение (19.4) представляет собой закон сохранения момента импульса: момент импульса замкнутой системы сохраняется, т. е. не изменяется с течением времени.
Закон сохранения момента импульса — фундаментальный закон природы. Он связан со свойством симметрии пространства — его изотропностью, т. е. с инвариантностью физических законов относительно выбора направления осей координат системы отсчета (относительно поворота замкнутой системы в пространстве на любой угол).
Продемонстрировать закон сохранения момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидящий на скамье, которая без трения вращается вокруг вертикальной оси, держит в вытянутых руках гантели (рис. 29). Если человек прижмет гантели к себе, то момент инерции системы уменьшится. А поскольку момент внешних сил равен нулю, и момент импульса системы сохраняется, угловая скорость вращения возрастает. Аналогично, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.
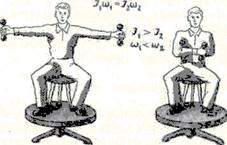
Рис. 29
Сопоставим основные величины и уравнения, определяющие вращение тела вокруг неподвижной оси и его поступательное движение (табл. 2).
Таблица 2
Масса 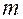 Скорость Скорость 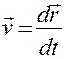 Ускорение Ускорение 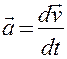 Сила Сила 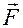 Импульс Импульс 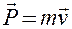 Основное уравнение динамики Основное уравнение динамики 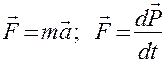 Работа Работа 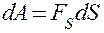 Кинетическая энергия Кинетическая энергия 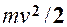 | Момент инерции 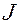 Угловая скорость Угловая скорость 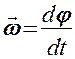 Угловое ускорение Угловое ускорение 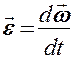 Момент силы Момент силы 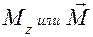 Момент импульса Момент импульса 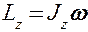 Основное уравнение динамики Основное уравнение динамики 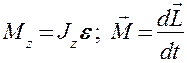 Работа вращения Работа вращения 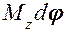 Кинетическая энергия вращения Кинетическая энергия вращения 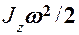 |
 2015-01-21
2015-01-21 3427
3427
