2015-01-21
802
а. С вероятностью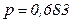 
.
Средняя ошибка репрезентативности выборочной средней:
,
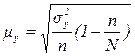где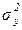 
– выборочная дисперсия (в задании 4 общая дисперсия определена: 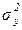=241);
n – численность выборочной совокупности, количество предприятий (n=40);
N – численность генеральной совокупности, количество предприятий (N=100 согласно данным приложения 1).
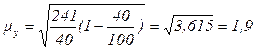млн. руб.
Предел для ошибки выборки с вероятностью 0,683:
,
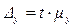где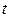 
– коэффициент кратности, связанный с вероятностью, гарантирующей результат: 
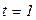– вероятность того, что предельная ошибка не выйдет за пределы средней ошибки 
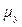, равна 0,683; 
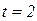– вероятность того, что предельная ошибка не превосходит двукратную среднюю ошибку 
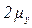, равна 0,954;
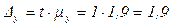млн. руб.
Границы генеральной средней величины с вероятностью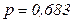 
:
,
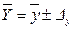где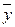 
– выборочная средняя величина (в задании 4 выборочная средняя определена: 
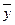=80 млн. руб.);
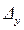– предельная ошибка выборочной средней, млн. руб.
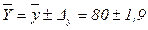млн. руб., т.е. 
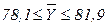млн. руб.
Ответ: с вероятностью 
(68,3%) можно утверждать, что в генеральной совокупности, состоящей из 100 предприятий, средний размер их балансовой прибыли находится в пределах от 78,1 до 81,9 млн. руб. В оставшихся 31,7 случаях из 100 (317 случаях из 1000) средний размер балансовой прибыли 100 предприятий может оставаться в указанных пределах или выходить за них.
б. С вероятностью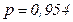 
.
Средняя ошибка репрезентативности выборочной средней:
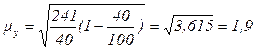млн. руб.
Предел для ошибки выборки с вероятностью :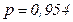
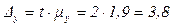млн. руб.
Границы генеральной средней с вероятностью :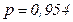
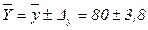млн. руб., т.е. 
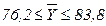млн. руб.
Ответ: с большой вероятностью (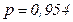 или 95,4%) можно утверждать, что в генеральной совокупности, состоящей из 100 предприятий, средний размер их балансовой прибыли находится в интервале от 76,2 до 83,8 млн. руб. В оставшихся 4,6 случаях из 100 (46 случаях из 1000) средний размер балансовой прибыли 100 предприятий может оставаться в указанных пределах или выходить за них.
