Прогнозирование по парной регрессионной модели

Под прогнозированием по парной регрессионной модели понимается нахождение неизвестных значений зависимой переменной для тех значений независимой переменной 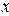, которых нет в исходных наблюдениях. Различают точечное и интервальное прогнозирование. В первом случае оценка – некоторое число, во втором – интервал, в котором находится истинное значение зависимой переменной с заданной вероятностью.

Прогностические способности модели определяются величиной индекса детерминации. О достаточном качестве прогноза можно говорить, как правило, лишь при значении коэффициента (индекса) детерминации, большем 0,75.

Точечный прогноз 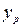результирующего признака y определяется путем подстановки в уравнение регрессии 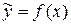значения x_p независимого фактора: 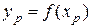. В случае линейной модели .

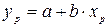Точечный прогноз явно не реален, поэтому он всегда дополняется расчетом доверительного интервала прогноза. В случае интервального прогнозапо парной линейной модели предварительно рассчитывается стандартная ошибка прогноза:

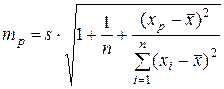, (3.5)

где .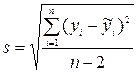

Затем строится доверительный интервал прогноза

,

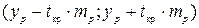т.е. определяются нижняя и верхняя границы интервала прогноза.

Из формулы (3.5) следует, что ширина доверительного интервала прогноза зависит от стандартной ошибки регрессии 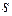(т.е. от качества модели), а также от значения x_p независимого фактора 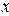, как это видно на рисунке 3.7: при 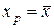она минимальна, а по мере удаления 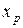от она увеличивается.

Отсюда следует, что интервальный прогноз реалистичен в пределах диапазона исходных данных. Экстраполяция кривой регрессии, т.е. ее использование вне пределов наблюдаемого диапазона значений объясняющей переменной, может привести к значительным погрешностям. Поэтому, в частности, долгосрочное прогнозирование по трендовым моделям, где в качестве независимой переменной выступает время, как правило, не оправдывает себя.

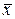
Рис. 3.7. Доверительная полоса линии регрессии