Оценки неизвестных параметров бывают двух видов - ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ.
ТОЧЕЧНАЯ ОЦЕНКА - оценка имеющая конкретное числовое значение. Например, среднее арифметическое:
X = (x1+x2+...+xn)/n,
где: X - среднее арифметическое (точечная оценка МО);
x1,x2,...xn - выборочные значения; n - объем выборки.
ИНТЕРВАЛЬНАЯ ОЦЕНКА - оценка представляемая интервалом значений, внутри которого с задаваемой исследователем вероятностью находится истинное значение оцениваемого параметра. Интервал в интервальной оценке называется ДОВЕРИТЕЛЬНЫМ ИНТЕРВАЛОМ, задаваемая исследователем вероятность называется ДОВЕРИТЕЛЬНОЙ ВЕРОЯТНОСТЬЮ. В практике статистических вычислений применяются стандартные значения доверительной вероятности: 0,95, 0,98 и 0,99 (95%, 98% и 99% соответственно). Например, интервальная оценка МО (3,8) при доверительной вероятности 0,95. Это означает, что МО лежит в пределах от 3 до 8 с вероятностью 0,95, следовательно вероятность того, что МО меньше 3 или больше 8 не превышает 0,05.
Очевидно, что чем выше доверительная вероятность, тем выше точность оценки, но шире доверительный интервал.Отсюда следует - ДЛЯ НЕПРЕРЫВНЫХ СЛУЧАЙНЫХ ВЕЛИЧИН ВЕРОЯТНОСТЬ ТОГО, ЧТО ТОЧЕЧНАЯ ОЦЕНКА (ширина доверительного интервала равна 0) СОВПАДЕТ С ЛЮБЫМ ЗАДАННЫМ ЗНАЧЕНИЕМ ИЛИ ОЦЕНИВАЕМЫМ ПАРАМЕТРОМ РАВНА 0.
Таким образом, точечная оценка имеет смысл лишь тогда, когда приведена характеристика рассеяния этой оценки (дисперсия).В противном случае она может служить лишь в качестве исходных данных для построения интервальной оценки.
Вычисление интервальной оценки рассмотрим на примере интервальной оценки МО для случайной величины подчиняющейся нормальному закону распределения. Границы доверительного интервала определятся по формулам:
Xmin = X - T(ν,P)*S/(n)1/2
Xmax = X + T(ν,P)*S/(n)1/2
где: Xmin, Xmax - нижняя и верхняя границы интервала;
X - среднее арифметическое (точечная оценка МО);
n - объем выборки;
T(ν,P) - поправочный коэффициент, называемый T-статистика, величина которого определяется значением задаваемой доверительной вероятности p и числом степеней свободы ν (ν=n-1);
S = [(x1 - X)2 + (x2 - X)2 +... + (xn - X)2]1/2 - корень квадратный из оценки дисперсии случайной величины X
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ СТАТИСТИКИ - число независимых случайных величин, по которым вычисляется данная статистика. Например, при вычислении среднего арифметического все случайные величины в выборке x1,x2,...,xn независят друг от друга. В оценке S из n отклонений вида (xi - X)2 независимы только n-1 (т.к. в формуле присутствует X, то по любому набору n-1 отклонений вычисляется n -ое).
Погрешности средств измерений и измерительных каналов средств автоматизации могут быть выражены двумя различными способами: с помощью точечных оценок и с помощью интервальных. К точечным оценкамотносится математическое ожидание погрешности и среднеквадратическое отклонение.В качестве интервальной оценкииспользуют интервал погрешности, который охватывает все возможные значения погрешности измерений с вероятностью  .Эта вероятность называется доверительной или надежностью оценки погрешности.
.Эта вероятность называется доверительной или надежностью оценки погрешности.
Предел допускаемой погрешности можно рассматривать как точечную оценку или как интервальную для доверительной вероятности, равной единице.
Интервальная оценка является более гибкой, поскольку она позволяет указать погрешность измерений в зависимости от того, какая требуется вероятность реализации этой погрешности для конкретных условий эксплуатации средства измерений.
Смысл интервальной оценки погрешности иллюстрируется рис. 4.3. Здесь использованы следующие обозначения:  - погрешность измерения;
- погрешность измерения; 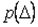 - плотность распределения погрешностей
- плотность распределения погрешностей  ;
;  - функция распределения погрешностей,
- функция распределения погрешностей,  .Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины
.Для нормального закона распределения погрешностей (закона Гаусса) плотность распределения центрированной случайной величины  описывается функцией
описывается функцией  , где
, где  - среднеквадратическая погрешность.
- среднеквадратическая погрешность.
Если погрешность измерения  находится внутри интервала
находится внутри интервала 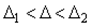 , то вероятность этого события вычисляется как
, то вероятность этого события вычисляется как
 . . | (4.35) |
В наиболее типичном случае симметричных границ ( ) получим
) получим
 . . | (4.36) |
Здесь использовано свойство симметрии функции распределения для закона Гаусса.
Таким образом, если задан интервал  , который содержит в себе погрешность измеряемого параметра
, который содержит в себе погрешность измеряемого параметра  , то вероятность того, что погрешность
, то вероятность того, что погрешность  не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность
не выходит за границы интервала, можно найти по формуле (4.36) для нормального закона распределения. Вероятность 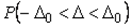 называют также надежностью оценки погрешности и обозначают символом
называют также надежностью оценки погрешности и обозначают символом 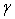 :
:
 . . | (4.37) |
Для вычисления функции распределения удобно использовать пакеты MathCAD, Matlab.С их помощью из формулы (4.37) несложно найти величину доверительного интервала  , если задана величина надежности
, если задана величина надежности 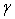 .
.
Для 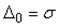 доверительная вероятность
доверительная вероятность 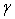 =68,3%; для
=68,3%; для 
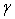 =95,3%; для
=95,3%; для 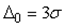
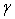 =99,7% и для
=99,7% и для 
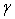 = 99,994%.
= 99,994%.
Для увеличения надежности оценки погрешности измерений или для сужения доверительного интервала при заданной надежности можно использовать усреднение результатов многократных измерений. Поскольку оценка среднеквадратической погрешности результата усреднения  равна
равна  (см. (3.2)), где
(см. (3.2)), где  - среднеквадратическая погрешность средства измерений,
- среднеквадратическая погрешность средства измерений, 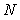 - количество однократных измерений, то, подставив в (4.37) вместо
- количество однократных измерений, то, подставив в (4.37) вместо  величину
величину  , получим
, получим
 . . | (4.38) |
Эта формула позволяет найти количество однократных измерений 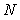 , которое необходимо усреднить для получения требуемого доверительного интервала
, которое необходимо усреднить для получения требуемого доверительного интервала  при заданной надежности
при заданной надежности 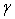 или требуемой надежности
или требуемой надежности 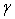 при заданном доверительном интервале
при заданном доверительном интервале  .Поскольку формула (4.38) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.
.Поскольку формула (4.38) задана в неявном виде, для нахождения требуемых неизвестных следует воспользоваться математическими пакетами для компьютерных вычислений.
Следует иметь в виду, что повышение точности путем усреднения результатов многократных измерений имеет множество ограничений.
Проблемой использования интервального метода оценки погрешности является необходимость знания закона распределения погрешностей.
 Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений.Систематическую погрешность или наличие ошибки в постановке эксперимента, в учете факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.
Отметим, что доверительные интервалы, полученные из рассеяния множества измерений, никак не учитывают систематическую погрешность измерений.Систематическую погрешность или наличие ошибки в постановке эксперимента, в учете факторов, о существовании которых мы не знаем, оценить невозможно, не имея более точного измерительного прибора.
Результат испытаний может быть дискретной или непрерывной случайной величиной.Так, количество дефектных изделий в выборке - дискретная случайная величина, поскольку это может быть только целое число.
Непрерывная случайная величина может принимать любое значение в некотором конечном или бесконечном интервале (например, разрывная длина бумаги).При испытаниях часто получают выборку значений непрерывной случайной величины с некоторым распределением вероятности получения того или иного значения.Наиболее часто встречается нормальное распределение.Точнее, реальные распределения в большинстве случаев достаточно близки к нормальному.
Основные параметры нормального распределения – математическое ожидание М случайной величины и её генеральное среднеквадратическое отклонение (СКО) σ (или генеральная дисперсия σ2).Математическое ожидание – это центр группировки результатов испытаний, при отсутствии систематических погрешностей соответствует количественной характеристике объекта испытаний.Дисперсия (или СКО) – мера рассеяния результатов испытаний.Найти их значения абсолютно точно невозможно. Однако при объёме выборки n не менее 25…30 обычно считают, что точечные оценки параметров нормального распределения с приемлемой точностью равны параметрам. Кроме того, можно достаточно точно рассчитать генеральную дисперсию при проведении серий испытаний, в которых генеральная дисперсия не меняется (вычисление дисперсии по текущим измерениям), например, при приёмо-сдаточных испытаниях.
Применяется также мера рассеяния, называемая коэффициентом вариации. Генеральный коэффициент вариации
γ=σ/M; (1.1)
Выборочный коэффициент вариации
 (1.2)
(1.2)
Точечной оценкой математического ожидания М является среднее значение выборки  :
:
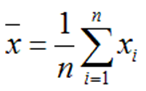
Точечной оценкой генеральной дисперсии является выборочная несмещенная дисперсия:
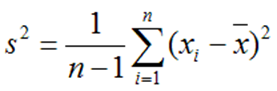
По текущим измерениям дисперсия может быть вычислена по формуле

Здесь ni – объем испытаний (объём выборки) в каждой серии, si2 – дисперсии в соответствующих сериях, m – количество серий.
Оценка генерального СКО - выборочное СКО:

Точечные оценки малоинформативны, поскольку являются случайными величинами и могут значительно отличаться от оцениваемо-го параметра.Для повышения информативности используют интер-вальные оценки (рассчитывают доверительные интервалы).
При достаточно точно известной генеральной дисперсии σ2) доверительный интервал для математического ожидания определяют из соотношения
 (1.3)
(1.3)
или

Здесь уровень значимости α=1-Р (Р -доверительная вероятность), z1-α/2 – квантиль стандартного нормального распределения, n – объём испытаний (объём выборки).
Если генеральная дисперсия неизвестна, доверительный интервал для математического ожидания определяют из соотношения
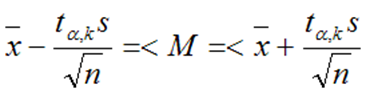
Здесь tα;k – коэффициент Стьюдента, k=n-1 – число степеней свободы. Доверительный интервал для дисперсии определяют из соотношения:
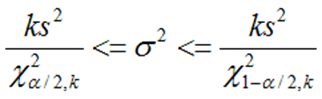
Здесь χ2 - критерий распределения хи-квадрат, k=n-1 – число степеней свободы.
Извлекая из всех частей неравенства квадратный корень, можно получить интервальную оценку СКО.



LU-метод
LU-разложение — это представление матрицы A в виде A=L•U, где L — нижнетреугольная матрица с еденичной диагональю, а U — верхнетреугольная матрица. LU-разложение является модификациеё метода Гаусса.Основные применения данного алгоритма — решение систем алгебраических уравнений, вычисление определителя, вычисление обратной матрицы и др.
Рассмотрим алгоритм на примере матрицы
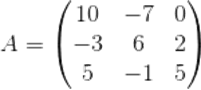
Алгоритм
1. Создаем матрицы

и

2. Для каждого столбца j = 1… 3 матрицы  будем вычислять
будем вычислять 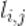 как
как

Для каждой строки  вычислим
вычислим 
Выполняем шаг 2 пока j<=3
3. Получем

и

Такие, что A=L•U
Результаты после каждого шага:
1. 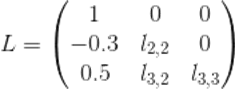

2. 

3. 

Проверкой удостоверяемся, что L*U=A
 2018-02-13
2018-02-13 19760
19760
