2015-01-21
2278
Теоре́ма о кинети́ческой эне́ргии систе́мы — одна из общих теорем динамики[1], является следствием законов Ньютона. Связывает кинетическую энергию механической системы с работой сил, действующих на тела, составляющие систему. В качестве системы, о которой идёт речь, может выступать любая механическая система, состоящая из любых тел[2][3].
Рассмотрим систему материальных точек с массами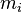 
, скоростями 
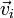и кинетическими энергиями 
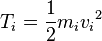. Для малого изменения кинетической энергии (дифференциала), происходящего в течение некоторого малого промежутка времени 
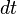, будет выполняться
Учитывая, что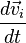 
представляет собой ускорение i -ой точки 
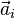, а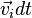 
— перемещение той же точки 
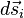за время 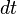, полученное выражение можно записать в виде:
Используя второй закон Ньютона и обозначая равнодействующую всех сил, действующих на точку, как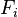 
, получаем
а затем в соответствии с определением работы 
Суммирование всех уравнений такого вида, записанных для каждой из материальных точек, приводит к формуле для изменения полной кинетической энергии системы:
Данное равенство выражает утверждение теоремы об изменении кинетической энергии системы в дифференциальном виде.
Проинтегрировав обе части полученного равенства по произвольно взятому промежутку времени между некоторым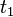и 
и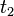 
, получим выражение теоремы об изменении кинетической энергии в интегральной форме:
где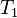 
и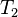 
— значения кинетической энергии системы в моменты времен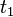и и 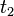соответственно.
Необходимо подчеркнуть, что здесь, в отличие от случаев теоремы об изменении количества движения системы и теоремы о движении центра масс системы, учитывается действие не только внешних, но внутренних сил.
