Распределение Ферми-Дирака. Уровень Ферми. Работа выхода электрона. Электронная эмиссия Контактные явления в металлах и полупроводниках

Сформулированная выше энергетическая модель кристалла носит общий характер. В пределах энергетической зоны не все уровни оказываются заняты или, говоря языком статистики, существует некоторая закономерность распределения электронов по энергиям.

У фермионов нет принципа неразличимости как у классических элементов статистической системы. Они различаются квантовыми числами. Это первое отличие

Постановка задачи..

Имеем термодинамическую систему из N невзаимодействующих частиц. Энергия частицы в

i-том состоянии 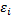. Система находится в равновесном состоянии T=Const.

Классическая постановка: Какова вероятность, что в этом состоянии находится 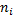частиц?

Квантовая интерпретация: Какова вероятность, что на данном энергетическом уровне 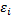находится один электрон и это состояние реализуется α способами (другие квантовые числа)?

Вторая особенность данной системы заключается в том, что при Т 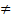0 число 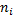может изменяться (переход на более низкие энергетические уровни без получения энергии из вне), то есть мы имеем т/д систему, состоящую из нескольких подсистем с изменяющимся числом частиц. Для описания таких систем следует воспользоваться большим распределением Гиббса. Равновесное состояние в таких системах достигается при равенстве температур и химических потенциалов µ.

Гамильтониан для таких систем имеет вид: 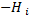=- – полная энергия частицы. Гамильтониан для подсистемы из 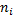идентичных элементов примет вид:

= .

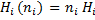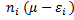Каноническое распределение Гиббса тогда можно записать:

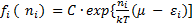– функция распределения вероятностей.

Это классическое распределение Гиббса для обозначенной выше системы. Постоянная С находится из условия нормировки:

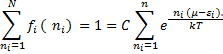
Применим полученное распределение к фермионам т.е для любого уровня 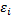имеем лишь два значения :

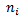0 или 1 (уровень свободен - или занят).

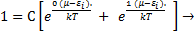C= .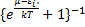

Теперь можно окончательно записать вероятность того, что состояние 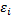занято (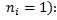

=

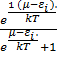
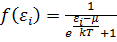
Это распределение Ферми –Дирака электронов по энергиям в квантовой системе.

Проведём анализ полученного результата.

1.В квантовой физике принято называть химический потенциал уровнем Ферми- 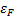Найдём его физический смысл.Пусть Т=0К.

Тогда для 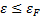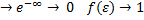Все уровни меньше (равные) уровня Ферми заняты.

При значениях энергии больший уровня Ферми уровни свободны.