8.1 Классификация вещества. Строение и общие свойства твёрдых тел.
По своим свойствам и строению твердые тела делятся на кристаллические и аморфные (стеклообразные).
Общие свойства: сохраняют форму, сопротивляются сжатию, сохраняют объём. Твёрдые тела состоят из атомов, между которыми действуют силы притяжения и отталкивания (электромагнитной природы). Это взаимодействие приводит к потере атомами своих индивидуальных свойств и возникновению новых коллективных свойств. Даже вещества с одинаковыми атомами, но с различным типом их взаимодействия могут значительно отличаться по своим механическим, электрическим и др. свойствам. Пример- сажа, алмаз, графен, углеродная нанотрубка.
Кристаллические тела наиболее изучены. Их структура отличается повторяемостью в пространстве.
Группа атомов, молекул или ионов образует некоторую элементарную конфигурацию, которая
периодически повторяется в трех измерениях без изменения своей ориентации. Таким образом, может быть
получен монокристалл макроскопических размеров с правильной внешней огранкой. При этом грани пересекаются под определенными для каждого вида кристалла углами.
Однако чаще всего объем кристалла бывает разбит на отдельные, разоориентированные относительно
друг друга области, в пределах которых ориентация элементарной конфигурации сохраняется. Такие
тела называются поликристаллическими.
Кристаллы образуются (растут) из расплавов, паров, растворов исходных веществ как в природных
условиях, так и в лабораторных.
В качестве примеров можно привести такие широко известные природные кристаллические мате-
риалы, как алмаз (С) и рубин (Al2O3), другие драгоценные камни, кварц (SiO2), каменную соль (NaCl),
различные металлы и их соединения.
Искусственно можно вырастить монокристаллы даже заданной ориентации. Для этого, например, в
расплав каменной соли, цинка и т.д. необходимо поместить небольшой образец кристалла определенной
ориентации (затравку) и медленно его из расплава вытягивать. В результате происходит кристаллизация и
образуется монокристалл с ориентацией затравки.
Кристаллические материалы в отличие от многих других веществ могут обладать анизотропией фи-
зических свойств (механических, электрических, оптических и др.), заключающихся в том, что эти
свойства зависят от выбранного в материале направления.
При независимости различных свойств от направления вещества изотропны. К ним относятся газы,
жидкости и аморфные тела (в переводе с греческого – бесформенные).
Кристаллы имеют определённую температуру плавления (отвердевания).
Аморфные тела представляют собой переохлажденные жидкости с большим коэффициентом вязко-
сти, препятствующим принятию более упорядоченной формы. Типичные представители данного класса
– стекло, различные полимеры, сажа и др. Они отличаются ближним порядком взаимодействия между
образующими их частицами. У кристаллов же – дальний порядок из-за периодичности их структуры.
Приведем образное выражение Дж. Блейкмора: «Поскольку степень упорядоченности аморфных
тел сильно зависит от условий их приготовления, можно предположить, что изучение аморфных тел в
отличие от кристаллов относится скорее к искусству, чем к науке». Однако интерес ученых к аморфным
телам весьма значителен в связи с наличием у них многих полезных свойств. Например, аморфный
кремний обладает ценными электронными свойствами.
Стеклообразные не имеют определённую температуру плавления (отвердевания).
ФИЗИЧЕСКИЕ ТИПЫ КРИСТАЛЛОВ.
Модели кристаллического тела, полно описывающей его свойства не существует. Упрощенные модели основываются на двух физических теориях: квантовой механике и статистической физике.
В основе физической классификации лежат различия в изменениях структуры атомных электронных оболочек в кристаллах. При этом электроны внешних оболочек атома (валентные)- рассматриваются как отдельные частицы. Ядро с внутренними оболочками электронов (ионный остав) - как единое целое.
Валентные электроны перестраивают свои орбитали в атомах кристалла так, что энергия атома в кристалле меньше, чем у изолированного. Так образуется различные типы связи узлов кристалла с различной энергией связи. Удельная энергия связи- это энергия, приходящиеся на один атом (молекулу).Она колеблется от 0,1 до 10 эВ/мол. Сильная связь 7-10 эВ/мол.
Различают четыре (иногда - пять) типа кристаллов в зависимости от типа связи и рода частиц в узлах кристаллической решетки.
1. Ионные кристаллы. В узлах кристаллической решетки расположены ионы противоположного зна-
ка. Типичные представители кристаллов данного типа являются каменная соль (NaCl), MgO и др.
В узлах кубической решетки NaCl чередуются положительные ионы натрия (Na +) и отрицательные
ионы хлора (Cl −). Между разноименно заряженными ионами существует ионная (гетерополярная) связь,
обусловленная их электростатическим взаимодействием. Если в газообразном состоянии NaCl состоит
из отдельных молекул, то в кристаллическом весь объем представляет собой как бы одну молекулу.
2. Атомные кристаллы. В узлах решетки расположены нейтральные атомы, которые связывает между
собой гомеополярная (ковалентная) связь квантово-механического происхождения. Эта связь образуется
взаимодействием пар электронов, которые обобществлены парами соседних атомов.
Типичными представителями данного класса являются алмаз и графит, а также полупроводниковые
материалы германий (Ge) и кремний (Si).
3. Металлические кристаллы. В узлах решетки – положительные ионы металла, между которыми хао-
тически движутся свободные электроны, образующие довольно однородное распределение отрицатель-
ного заряда в решетке. Между одноименно заряженными ионами существуют силы электростатическо-
го отталкивания, которые нейтрализуются зарядами свободных электронов. В результате ионы металла
оказываются на расстояниях друг от друга, соответствующих условию равновесия, и кристаллическая
решетка становится стабильной (устойчивой).
4. Молекулярные кристаллы. В узлах решетки – нейтральные молекулы. Силы связи обусловлены ван-дер-ваальсовским взаимодействием, которое является слабым и имеет место между близко расположенными нейтральными атомами и молекулами, проявляется при отсутствии других, более сильных, видов взаимодействия.
Ван-дер-ваальсовское взаимодействие может иметь дисперсионный, ориентационный (деформаци-
онный) и индукционный характер.
Дисперсионные силы возникают в исходно неполярных атомах и молекулах вследствие согласован-
ного движения электронов в соседних атомах при их сближении. Если электроны двух атомов оказываются по одну сторону от своих положительно заряженных ядер, то это эквивалентно образованию двух мгновенных притягивающихся электрических диполей. Если электроны при своем согласованном движении оказываются по разную сторону от ядра, то диполи отталкиваются. Механизм согласования основывается на том, что мгновенный диполь одного атома поляризует другой атом и создает, таким образом, наведенный диполь.
Ориентационный характер объясняется электростатическими силами взаимодействия между поляр-
ными молекулами, приводящими к их переориентации и деформации кристалла.
Индукционное взаимодействие происходит у полярных молекул с высокой степенью поляризуемо-
сти вследствие образования наведенного дипольного момента от поля постоянных диполей соседних
молекул.
К молекулярным кристаллам относятся многие вещества, например, такие, как кристаллы инерт-
ных газов (Ne, Ar, Kr, Xe), многих насыщенных органических соединений, в твердом состоянии Н2,
N2, O2, F2, CO2, H2O и др.
5. Водородная связь. Атом водорода, потерявший единственный электрон (по сути протон) способен удерживать два отрицательных иона другого вещества в структуре твёрдого тела. Например –фтора, кислорода, азота. Водородная связь важна в биологических структурах (таких как ДНК).
Этой связи обязаны удивительные свойства воды и льда.
8.2 Квантовое представление твердого тела. Модель атома Резерфорда-Бора. Функция Шрёдингера, волновое уравнение Шрёдингера. Потенциальная яма и потенциальный барьер. Простейшие решения волнового уравнения. Пространственная и энергетическая модель кристалла.
Затруднения классических представлений.
Классическая теория не смогла объяснить:
– устойчивость атомно-молекулярной структуры;
- закономерности излучения твёрдых тел, жидкостей, газов.
Требовались новые подходы и теории. Они формулировались в течение некоторого времени и основывались:
1) на классических законах -сохранения энергии, импульса, момента импульса, заряда, выводах СТО и др.;
2) на новых гипотезах и идеях––корпускулярно-волновой дуализм, дискретность и вероятностный характер значений параметров в микромире, соотношения неопределённости, принцип исключения Паули и др.
Квантовая модель твёрдого тела базируется на квантовых моделях атома. Это прежде всего:
-- пространственная модель. Корпускулярно-волновой дуализм предполагает новые уравнения движения (поведения) квантовой частицы, и, прежде всего, вероятностный характер обнаружения частицы в заданной точке пространства, а не её точные координаты. Решение уравнения Шрёдингера дало результаты не объясняемые с точки зрения классических представлений, в то же время подтверждаемые экспериментально.
-энергетическая модель. Основывается не только на дискретности энергетических уровней квантовых частиц, но и на вероятностном характере распределения по энергиям, с учётом новых принципов (принцип Паули, запрещённых энергетических зон и др.)
Модель атома Резерфорда-Бора.
Пространственная модель по Резерфорду – это планетарная модель, дополненная Н.Бором гипотезой о стационарных круговых орбитах электронов в атоме с дискретными радиусами:
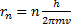 = n
= n 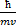 , где
, где 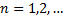 (1)
(1)
Энергетическая модель: излучение (поглощение) энергии происходит только при переходе электрона с одной стационарной орбиты на другую: 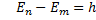 ν. (энергия дискретна)
ν. (энергия дискретна)
Уже в таком виде теория Бора объясняла найденные к тому времени сериальные закономерности в спектре излучения атомов водорода:
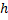 ν = R
ν = R 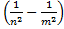 , здесь R- постоянная Ридберга, n, m –главные квантовые числа.
, здесь R- постоянная Ридберга, n, m –главные квантовые числа.
 представления о свете дали блестящее объяснение экспериментальным закономерностям в явлениях фотоэффекта, спектра излучения абсолютно черного тела.
представления о свете дали блестящее объяснение экспериментальным закономерностям в явлениях фотоэффекта, спектра излучения абсолютно черного тела.
 электромагнитной теорией об излучении энергии заряженной частицей.
электромагнитной теорией об излучении энергии заряженной частицей.
 , не было разрешено.
, не было разрешено.
 фотон, квант световой энергии, имеет двойственную природу. Импульс фотона
фотон, квант световой энергии, имеет двойственную природу. Импульс фотона 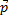 =
= 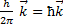 , где
, где 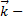 волновой вектор, совпадающий с направлением вектора импульса фотона как частицы.
волновой вектор, совпадающий с направлением вектора импульса фотона как частицы.
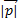 =
= 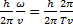 =
=  ,
,
где 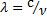 - длина волны излучения,
- длина волны излучения, 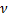 - частота, с- скорость распространения.
- частота, с- скорость распространения.
 высказал предположение, что корпускулярно - волновой дуализм присущ и другим частицам.
высказал предположение, что корпускулярно - волновой дуализм присущ и другим частицам. 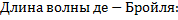

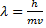 =
= 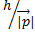 -связывает волновые и корпускулярные параметры частицы.
-связывает волновые и корпускулярные параметры частицы.
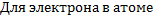 оказалось, что стационарные орбиты соответствуют окружностям, на длине которых укладывается целое число длин волн электрона как волны.
оказалось, что стационарные орбиты соответствуют окружностям, на длине которых укладывается целое число длин волн электрона как волны.
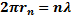
Электрон на стационарной орбите представляет собой заряженное кольцо. Такой объект при вращении не излучает и по законам электродинамики! Так был решен вопрос с устойчивостью атома как электродинамической системы.
Однако, как это часто бывает в науке, решение одной проблемы ставит много нерешённых других.
Для атома это проблема нахождения положения электрона, описание его движения с течением времени.
Для частиц в классической механике существует дифференциальное уравнение второго порядка –второй закон Ньютона:
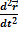 =
= 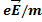 -- здесь eE- сила, действующая на электрон, m- его масса..
-- здесь eE- сила, действующая на электрон, m- его масса..
Движение э  как волны должно описываться волновым уравнением. Если решение уравнения Ньютона даёт однозначное значение радиус-вектора электрона-частицы (точные координаты), то точное значение положения электрона-волны, в принципе невозможно. Вместо радиуса-вектора должен быть введен другой параметр, изменение которого в пространстве и времени описывает движение электрона-волны.
как волны должно описываться волновым уравнением. Если решение уравнения Ньютона даёт однозначное значение радиус-вектора электрона-частицы (точные координаты), то точное значение положения электрона-волны, в принципе невозможно. Вместо радиуса-вектора должен быть введен другой параметр, изменение которого в пространстве и времени описывает движение электрона-волны.
Решить это проблему удалось Шрёдингеру. Введённая им функция 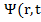 ) является функцией координат и времени и обладает волновыми свойствами. Квадрат её модуля пропорционален вероятности обнаружить частицу-волну в данной точке пространства и в заданный момент времени.
) является функцией координат и времени и обладает волновыми свойствами. Квадрат её модуля пропорционален вероятности обнаружить частицу-волну в данной точке пространства и в заданный момент времени.
Дифференциальное волновое уравнение движения (аналог уравнению Ньютона) имеет вид:
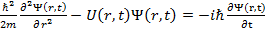 (2)
(2)
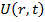 - потенциальная энергия частицы в силовом поле.
- потенциальная энергия частицы в силовом поле.
Для электрона в атоме (например, водорода) потенциальная энергия электрона не зависит от времени:
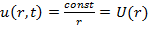 = -
= - 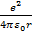 . (рис.1)
. (рис.1)
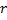 |
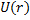 |
 |
 |
 – потенциальная яма – потенциальная яма |
 |
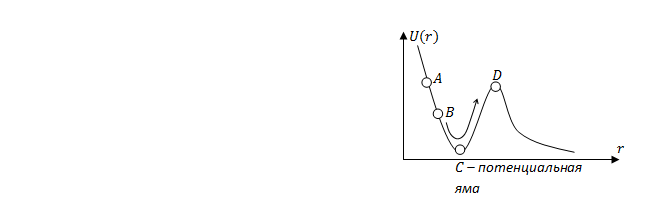
Пусть зависимость 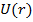 имеет вид (рис.2.)
имеет вид (рис.2.)
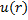 |
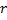 |
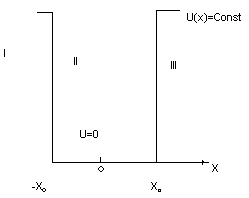
Рис.1 рис.2
Участок потенциального поля в окрестности точки С называют— потенциальная яма.
Вокрестности точки D - потенциальный барьер.
Механическая модель – шарик на кривой поверхности типа американской горки. Свободно скатываясь из точки А, шарик преодолеет барьер, а из точки В- нет. Это классическая трактовка превращения механической энергии.
Решим задачу движения электрона в потенциальном поле, близком к полю в атоме.
Введем следующие упрощения:
· потенциальную яму атома апроксимируем прямоугольной с высокими (очень высокими) стенкими (бесконечно большой барьер);
· потенциальная энергия зависит только от координаты x и не зависит от времени (одномерная потенциальная яма с бесконечными стенками);
· на дне ямы положим U(0)=0, за пределами ямы U( 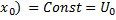 ..
..
Так как потенциальная энергия зависит только от координаты, то функцию Шрёдингера можно представить в виде произведения двух функций:
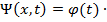 ψ(x) (3)
ψ(x) (3)
Подставим (3) в уравнение (2) и разделим на это произведение функций.
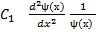 -– U(x) =
-– U(x) = 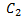
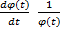 (4) Здесь
(4) Здесь 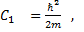
 . Нетрудно заметить, что левая часть уравнения (4) зависит только от координаты,а правая- только от времени. Это означает, что они равны одной и той же константе. Пусть эта постоянная равна –Е. (минус Е).
. Нетрудно заметить, что левая часть уравнения (4) зависит только от координаты,а правая- только от времени. Это означает, что они равны одной и той же константе. Пусть эта постоянная равна –Е. (минус Е).
Тогда (4) распадётся на два уравнения:
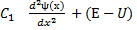
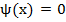 (5)
(5)
 = -–
= -– 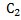
 E
E 
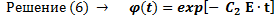 (7)
(7)
Уравнение (5) в области II (где U= 0) – примет вид уравнения колебаний в канонической форме:: 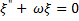
Решение: ψ(x) = A Sin 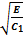 x + B Cos
x + B Cos 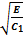 x. (8)
x. (8)
В областях I и III имеем U(x) 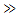 Е, уравнение (5) имеет другой вид и решение:
Е, уравнение (5) имеет другой вид и решение:
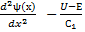
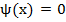
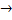 решение:
решение:
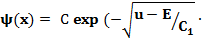 x) + D exp
x) + D exp 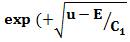
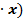 (9)
(9)
 нахождение постоянных интегрирования А,В,С,D из начальных и граничных условий и «сшивание» решений на границе областей II и III, ограничимся некоторыми выводами.
нахождение постоянных интегрирования А,В,С,D из начальных и граничных условий и «сшивание» решений на границе областей II и III, ограничимся некоторыми выводами.
1. 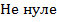 вое решение (8) будет лишь в том случае, когда функции синуса и косинуса не обращаются в ноль одновременно. Аргументы функций
вое решение (8) будет лишь в том случае, когда функции синуса и косинуса не обращаются в ноль одновременно. Аргументы функций
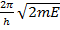 = n
= n 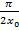 При любом целом значении n имеем не нулевое решение (при чётном n – одна функция, при нечётном –другая). Постоянная Е имеет смысл полной энергии частицы:
При любом целом значении n имеем не нулевое решение (при чётном n – одна функция, при нечётном –другая). Постоянная Е имеет смысл полной энергии частицы:
Е = 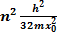 Энергияэлектрона в атоме квантована!Этотрезультат получен не на основании гипотезы, а в результате решения уравнения, описывающего поведение частицы.
Энергияэлектрона в атоме квантована!Этотрезультат получен не на основании гипотезы, а в результате решения уравнения, описывающего поведение частицы.
2. Если найти интеграл от квадрата модуля функции Шрёдингера от 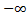 до +
до + 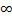 , то он равен 1.
, то он равен 1.
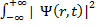 dr =1 то есть квадрат модуля функции Шрёдингера ведет себя как функция плотности вероятности. Вероятность обнаружить квантовую частицу в некоторой точке (области) пространства есть
dr =1 то есть квадрат модуля функции Шрёдингера ведет себя как функция плотности вероятности. Вероятность обнаружить квантовую частицу в некоторой точке (области) пространства есть
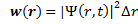
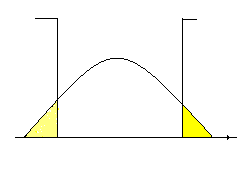
 Требование сшивания решений на границах областей даёт отличное от нуля значения функции Шрёдингера за пределами потенциальной ямы. Это означает, что частица с энергией меньше высоты потенциального барьера имеет вероятность отличную от нуля находиться за пределами потенциальной ямы. Такого классическая механика не разрешает, иначе нарушается закон (классический) сохранения энергии.
Требование сшивания решений на границах областей даёт отличное от нуля значения функции Шрёдингера за пределами потенциальной ямы. Это означает, что частица с энергией меньше высоты потенциального барьера имеет вероятность отличную от нуля находиться за пределами потенциальной ямы. Такого классическая механика не разрешает, иначе нарушается закон (классический) сохранения энергии.  чисто квантовое явление называется туннельным эффектом.
чисто квантовое явление называется туннельным эффектом.
 подтверждён экспериментом, но и создано множество приборов на основе этого эффекта.
подтверждён экспериментом, но и создано множество приборов на основе этого эффекта.
Многоэлектронные атомы.Квантовые числа. Пространственная и энергетическая модель кристалла.
Все рассмотренное выше было верно для атома водорода, но для многоэлектронных атомов необходимо провести корректировку. Для атома водорода было достаточно главного квантового числа 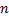 и спинового, чтобы удовлетворить принципу исключения Паули. Для многоэлектронных атомов необходимо ввести азимутальное квантовое число
и спинового, чтобы удовлетворить принципу исключения Паули. Для многоэлектронных атомов необходимо ввести азимутальное квантовое число 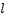 , которое характеризует форму орбиты (
, которое характеризует форму орбиты (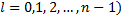 . и магнитное квантовое число
. и магнитное квантовое число 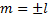 -определяет ориентацию орбиты.
-определяет ориентацию орбиты.
Все это обусловлено тем фактом, что сложные атомы (молекулы) требуют квантования не только по энергии, но и по другим физическим величинам, в том числе и по импульсу, магнитному моменту и др.
Принцип Паули: в одной квантовой системе не может быть двух электронов с одинаковым набором квантовых чисел.
В другом исполнении этот принцип звучит как: два и более тождественных фермиона не могут находиться в одном квантовом состоянии. Фермион – это частица с полуцелым значением спина (собственного момента импульса  .=
.= 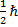 .
.
Фермионы подчиняются статистике Ферми-Дирака, которая как раз и говорит о том, что сказано в принципе запрета Паули. Этот принцип объясняет стабильность электронных оболочек атомов, делая возможным существование сложных химических элементов. Отметим, что принципе запрета Паули также следует из решений волнового уравнения Шрёдингера. Таким образом, состояние квантовой системы определяется четырьмя квантовыми числами: n,  ,m,s,
,m,s,
Электроны внутри атома (молекулы) образуют оболочки: n=1 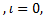 ,m=0, s=
,m=0, s= 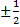 , только два электрона могут находиться на первой к ядру оболочке, К-оболочке. Для n=2 набирается уже 8 электронов, это
, только два электрона могут находиться на первой к ядру оболочке, К-оболочке. Для n=2 набирается уже 8 электронов, это
L-оболочка. Формула для числа электронов в n-состоянии Z=2n2
При соединении атомов в молекулу, ячейку кристалла, кристалл- квантовой системой становится соответствующее объединение взаимодействующих частиц (элементов системы) и все квантовые законы и принципы распространяются на всю эту систему. Число атомов в единице объёма громадно 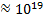 1/см3.
1/см3.
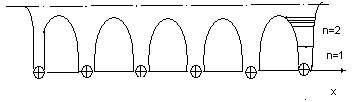
Пространственная модель кристалла. Потенциальные кривые становятся замкнутыми и изменяются с периодичностью чередования узлов решётки. На границе с вакуумом потенциальные кривые становятся выше, что соответствует внешней контактной разности потенциалов, определяющей работу выхода.)
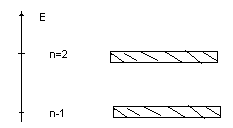 Энергетическая модель: уровни в каждом n-состоянии распадаются настолько близких значений, сколько необходимо для удовлетворения принципа Паули (порядки числа электронов в кристалле). Эти уровни становятся практически не различимы и можно говорить об образовании энергетических зон для каждого значения главного квантового числа.
Энергетическая модель: уровни в каждом n-состоянии распадаются настолько близких значений, сколько необходимо для удовлетворения принципа Паули (порядки числа электронов в кристалле). Эти уровни становятся практически не различимы и можно говорить об образовании энергетических зон для каждого значения главного квантового числа.
Обычно проводят более крупное деление на зоны:
энергетическая зона валентных электронов;
зонаэлектронов проводимости (свободных электронов).
В каждой зоне могут быть интервалы энергий, которую
не могут принимать электроны. Это запрещенные зоны.
По ширине запрещённой зоны между валентной и свободной проводиться классификация проводимости веществ.
 2015-01-21
2015-01-21 1167
1167








