| 1. Непосредственное интегрирование | 2. Замена переменной (подстановка) | 3. Интегрирование по частям | ||
Выполняется:
1. По таблице интегралов и свойствам:
а) 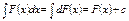 б)
б) 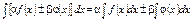 в)
в) 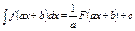 2. С использованием преобразований:
а) почленное деление; б) выделение целой части;
в) применение тригонометрических тождеств г) выделение полного квадрата
2. С использованием преобразований:
а) почленное деление; б) выделение целой части;
в) применение тригонометрических тождеств г) выделение полного квадрата
| Применяется:
1. При интегрировании некоторых классов функций:
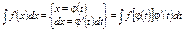 .
2. При наличии дифференциальной связи: .
2. При наличии дифференциальной связи:
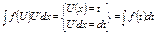 (за новую переменную принимают функцию, от которой в подинтегральном выражении есть дифференциал)
(за новую переменную принимают функцию, от которой в подинтегральном выражении есть дифференциал)
| 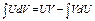 1.
1. 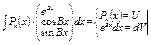 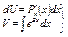 2.
2. 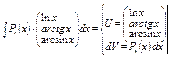 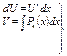
| ||
| 4. Стандартные приемы и подстановки при интегрировании некоторых классов функций | ||||
| а) рациональные дроби | б) тригонометрические выражения | в) иррациональные выражения | ||
1. Простейшие дроби
I. 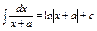 . II. . II. 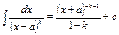 .
III. .
III. 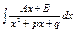 . IV. . IV. 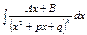 , , 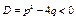 .
Алгоритм преобразования дробей вида III и IV:
1) Выделить полный квадрат: .
Алгоритм преобразования дробей вида III и IV:
1) Выделить полный квадрат: 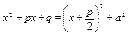 2) Применить подстановку:
2) Применить подстановку: 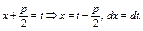 3) Разложить на два интеграла вида: 7а, 11 (табличные).
4) Для дроби вида IV применить формулу:
3) Разложить на два интеграла вида: 7а, 11 (табличные).
4) Для дроби вида IV применить формулу:
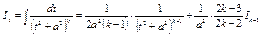 .
2. Рациональные дроби вида .
2. Рациональные дроби вида 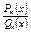 Алгоритм интегрирования:
1. Если дробь неправильная
Алгоритм интегрирования:
1. Если дробь неправильная 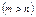 , то выделить целую часть.
2. Разложить знаменатель , то выделить целую часть.
2. Разложить знаменатель 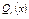 на простые множители: на простые множители:
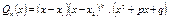 .
3. Правильную дробь разложить на сумму простейших дробей .
3. Правильную дробь разложить на сумму простейших дробей
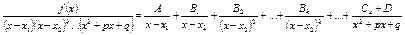 (*)
4. Привести правую часть равенства (*) к общему знаменателю и уравнять числители левой и полученной правой частей
5. Найти коэффициенты (*)
4. Привести правую часть равенства (*) к общему знаменателю и уравнять числители левой и полученной правой частей
5. Найти коэффициенты 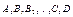 , применив к целому выражению:
а) метод частных значений , применив к целому выражению:
а) метод частных значений 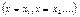 ;
б) метод сравнения коэффициентов при одинаковых степенях;
6. Проинтегрировать простейшие дроби. ;
б) метод сравнения коэффициентов при одинаковых степенях;
6. Проинтегрировать простейшие дроби.
| Универсальная подстановка
1. 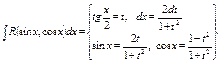 Частные случаи:
1.1.
Частные случаи:
1.1. 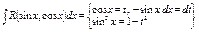
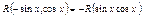 - нечетная относительно « - нечетная относительно «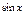 »
1.2. »
1.2. 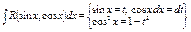
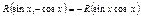 -
нечетная относительно « -
нечетная относительно «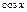 »
1.3. »
1.3. 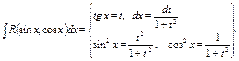
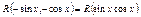 - четная в совокупности.
2. - четная в совокупности.
2. 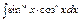 , где , где 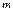 и и 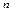 четные, четные, 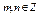 Применить формулы понижения:
Применить формулы понижения:
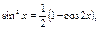 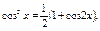 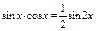 3.
3. 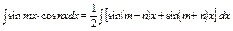
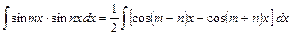
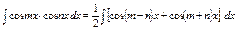 4.
4. 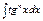 , , 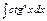 Применяется:
Применяется: 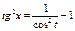 , , 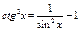
| 1. Линейная иррациональность
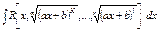
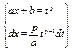 , где , где 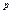 - наименьший общий
знаменатель - наименьший общий
знаменатель 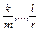 2. Квадратичные иррациональности.
2.1.
2. Квадратичные иррациональности.
2.1.
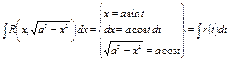 2.2.
2.2.
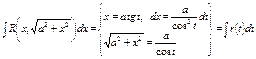 2.3.
2.3.
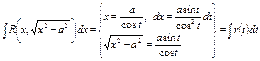 3.
3. 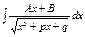 Смотри алгоритм интегрирования дроби вида III.
Сводится к интегралам 1, 9, 18 таблицы №2
4.
Смотри алгоритм интегрирования дроби вида III.
Сводится к интегралам 1, 9, 18 таблицы №2
4. 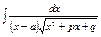 , ,
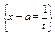 - обратная подстановка. - обратная подстановка.
| ||
Методы интегрирования
|
|

Сейчас читают про:
 2015-01-21
2015-01-21 367
367







