В случае бесповторной выборки СВ 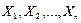 будут зависимыми.
будут зависимыми.
Теорема. Выборочная доля 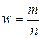 бесповторной выборки есть несмещенная и состоятельная оценка генеральной доли
бесповторной выборки есть несмещенная и состоятельная оценка генеральной доли 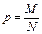 , причем ее дисперсия:
, причем ее дисперсия:
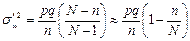 .
.
☺ Очевидно, что и для бесповторной выборки 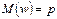 , т.е. w - несмещенная оценка для генеральной доли
, т.е. w - несмещенная оценка для генеральной доли 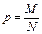 . Это связано с тем, что мат-кое ожидание суммы любых случайных величин равно сумме их мат-ких ожиданий (в том числе суммы зависимых случайных величин, каковой является выборочная доля w бесповторной выборки).
. Это связано с тем, что мат-кое ожидание суммы любых случайных величин равно сумме их мат-ких ожиданий (в том числе суммы зависимых случайных величин, каковой является выборочная доля w бесповторной выборки).
Найдем дисперсию выборочной доли для бесповторной выборки:
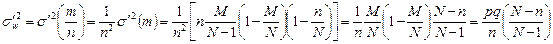 ,
,
При выводе формулы использовали то, что СВ Х = m в случае бесповтoрной выборки имеет гипергеометрическое распределение, и ее дисперсия определяется по формуле 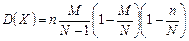 .
.
38. Оценка генеральной средней по собственно-случайной выборке. Несмещенность и состоятельность выборочной средней.
Пусть из генеральной совокупности объема N отобрана случайная выборка 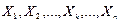 , где Xk - СВ, выражающая значение признака у k-гo элемента выборки (k=1,2,...,n). Следует найти «наилучшую» оценку для генеральной средней.
, где Xk - СВ, выражающая значение признака у k-гo элемента выборки (k=1,2,...,n). Следует найти «наилучшую» оценку для генеральной средней.
Рассмотрим в качестве такой возможной оценки выборочнyю среднюю х, т.е. 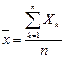 .
.
 2015-01-21
2015-01-21 722
722








