Закон распределения для каждой случайной величины 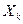 (k=1,2,...,n) имеет вид:
(k=1,2,...,n) имеет вид:
 Случайные величины
Случайные величины 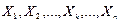 независимы, т.к. независимы любые события
независимы, т.к. независимы любые события 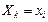 (k=1,2,...n; i=1,2,...,m) и их комбинации.
(k=1,2,...n; i=1,2,...,m) и их комбинации.
Найдем числовые характеристики СВ 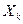 :
:
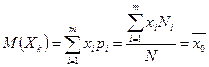 , (1)
, (1)
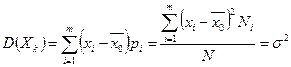 . (2)
. (2)
т.е. мат-кое ожидание и дисперсия каждой СВ 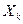 - это соот-но генеральная средняя и генеральная дисперсия.
- это соот-но генеральная средняя и генеральная дисперсия.
Теорема. Выборочная средняя 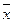 повторной выборки есть несмещенная и состоятельная оценка генеральной средней
повторной выборки есть несмещенная и состоятельная оценка генеральной средней 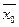 причем
причем 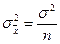 .
.
□ Докажем вначале несмещенность оценки. Найдем мат-кое ожидание выборочной средней 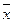 , учитывая (2) и то, что
, учитывая (2) и то, что 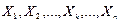 - независимые случайные величины:
- независимые случайные величины:
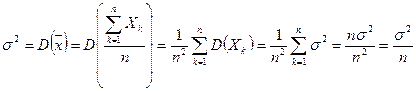 .
.
Осталось доказать состоятельность оценки 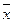 , которая следует непосредственно из теоремы Чебышева:
, которая следует непосредственно из теоремы Чебышева: 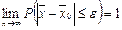 или
или 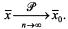
 2015-01-21
2015-01-21 938
938








