Б) Выборка бесповторная

Для бесповторной выборки 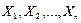- зависимые случайные величины. Можно показать, что

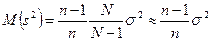(т.к. объем генеральной совокупности N, как правило, большой и N ≈ N -1).

Итак, и для повторной выборки, и для бесповторной 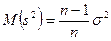, т.е 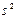- смещенная оценка . ▲

Т.к. 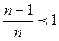и 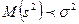, то выборочная дисперсия (в n среднем, полученная по разным выборкам) занижает генеральную дисперсию. Поэтому, заменяя на 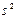, мы допускаем систематическую погрешность в меньшую сторону. Чтобы ее ликвидировать, достаточно ввести поправку, умножив 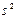на 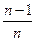. Тогда с учетом (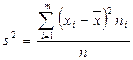) получим «исправленную» выборочную дисперсию:

.

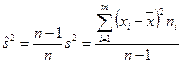Очевидно, что .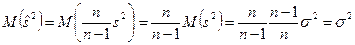

Т.е. 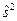является несмещенной и состоятельной оценкой генеральной дисперсии .

40. Понятие об интервальном оценивании. Доверительная ве­роятность и доверительный интервал. Предельная ошибка выбор­ки. Ошибки репрезентативности выборки (случайные и систематические).

Интервальной оценкой параметра θ называется числовой интервал 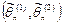, к-ый с заданной вероятностью γ накрывает неизвестное значение параметра θ.

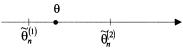
Обращаем внимание на то, что границы интервала и его величина находятся по выборочным данным и потому являются случайными величинами в отличие от оцениваемого параметра θ - величины неслучайной, поэтому правильнее говорить о том, что интервал «накрывает», а не «содержит» значение θ.

Такой интервал 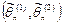называется доверительным, а вер-ть γ - доверительной вер-тью, уровнем доверия или надежностью оценки.

Величина доверительного интервала существенно зависит от объема выборки n (уменьшается с ростом n) и от значения доверительной вер-ти γ (увеличивается с приближением γ к 1).

Очень часто (но не всегда) доверительный интервал выбирается симметричным относительно параметра θ, т.е. (θ-Δ,θ+Δ).

Наибольшее отклонение Δ оценки 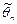от оцениваемого параметра θ, в частности, выборочной средней (или доли) от генеральной средней (или доли), к-ое возможно с заданной доверительной вер-тью γ, называется предельной ошибкой выборки.

Ошибка Δ является ошибкой репрезентативности (представительства) выборки. Она возникает только вследствие того, что исследуется не вся совок-ть, а лишь часть, ее (выборка), отобранная случайно. Эту ошибку часто называют случайной ошибкой репрезентативности. Ее не следует путать с систематической ошибкой репрезентативности, появляющейся в рез-те нарушения принципа случайности при отборе элементов в выборку.

41. Формула доверительной вероятности при оценке генеральной доли признака. Средняя квадратическая ошибка повторной и бесповторной выборок и построение доверительного интервала для генеральной доли признака.

42. Формула доверительной вероятности при оценке генеральной средней. Средняя квадратическая ошибка повторной и бес­повторной выборок и построение доверительного интервала для генеральной средней.

Построение доверительного интервала для гeнеральной средней и гeнеральной доли по большим выборкам. Для построения доверительных интервалов для параметров генеральных совокупностей м.б. реализованы 2 подхода, основанных на знании точного (при данном объеме выборки n) или асимптотического (при n → ∞) распределения выборочных характеристик (или некоторых функций от них). Первый подход реализован далее при построении интервальных оценок параметров для малых выборок. В данном параграфе рассматривается второй подход, применимый для больших выборок (порядка сотен наблюдений).

Теорема. Вер-ть того, что отклонение выборочной средней (или доли) от генеральной средней (или доли) не превзойдет число Δ > 0 (по абсолютной величине), равна: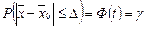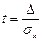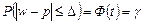

Где

, Где .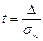

Ф(t) - функция (интеграл вероятностей) Лапласа.

Формулы получили название формул доверительной вер-ти для средней и доли.

Среднее квадратическое отклонение выборочной средней 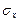и выборочной доли 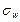собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки (для бесповторной выборки обозначаем соответственно 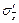и ).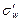

Следствие 1. При заданной доверительной вер-ти γ предельная ошибка выборки равна t-кратной величине средней квадратической ошибки, где Ф(t) = γ, т.е.

,

.

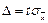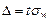Следствие 2. Интервальные оценки (доверительные интервалы) для генеральной средней и генеральной доли могут быть найдены по формулам:

,

.

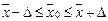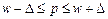43. Определение необходимого объема повторной и бесповтор­ной выборок при оценке генеральной средней и доли.

Для проведения выборочного наблюдения весьма важно правильно установить объем выборки n, к-ый в значительной степени определяет необходимые при этом временные, трудовые и стоимостные затраты для определения n необходимо задать надежность (доверительную вер-ть) оценки γ и точность (предельную ошибку выборки) Δ.

Если найден объем повторной выборки n, то объем соответствующей бесповторной выборки n' можно определить по формуле:

.

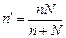Т.к. 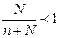, то при одних и тех же точности и надежности оценок объем бесповторной выборки n' всегда меньше объема повторной выборки n.

44. Статистическая гипотеза и статистический критерий. Ошибки 1-го и 2-го рода. Уровень значимости и мощность критерия. Принцип практической уверенности.

Определение. Статистической гипотезой называется любое предположение о виде или параметрах неизвестного закона распределения.

Различают простую и сложную статистические гипотезы. Простая гипотеза, в отличие от сложной, полностью определяет теоретическую функцию распределения СВ.

Проверяемую гипотезу обычно называют нулевой (или основной) и обозначают Н₀. Наряду с нулевой гипотезой рассматривают альтернативную, или конкурирующую, гипотезу H₁, являющуюся логическим отрицанием Н₀. Нулевая и альтернативная гипотезы представляют собой 2 возможности выбора, осуществляемого в задачах проверки статистических гипотез.

Суть проверки статистической гипотезы заключается в том, что используется специально составленная выборочная характеристика (статистика) 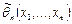, полученная по выборке 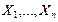, точное или приближенное распределение которой известно.

Затем по этому выборочному распределению определяется критическое значение 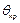- такое, что если гипотеза Н₀ верна, то вер-ть 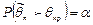мала; так что в соответствии с принципом практической уверенности в условиях данного исследования событие 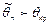можно (с некоторым риском) считать практически невозможным. Поэтому, если в данном конкретном случае обнаруживается отклонение 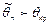, то гипотеза Н₀ отвергается, в то время как появление значения 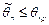, считается совместимым с гипотезой Н₀, которая тогда принимается (точнее, не отвергается). Правило, по которому гипотеза Н₀ отвергается или принимается, называется статистическим критерием или статистическим тестом.

Принцип практической уверенности:

Если вер-ть события А в данном испытании очень мала, то при однократном выполнении испытания можно быть уверенным в том, что событие А не произойдет, и в практической д-ти вести себя так, как будто событие А вообще невозможно.

Т.о., множество возможных значений статистики - критерия (критической статистики) 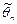разбивается на 2 непересекающихся подмножества: критическую область (область отклонения гипотезы) W и область допустимых значений (область принятия гипотезы) 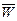. Если фактически наблюдаемое значение статистики критерия 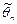попадает в критическую область W, то гипотезу Н₀ отвергают. При этом возможны четыре случая:

Определение. Вероятность α допустить ошибку l-го рода, т.е. отвергнуть гипотезу Н₀, когда она верна, называется уровнем значимости, или размером критерия.

Вероятность допустить ошибку 2-го рода, т.е. принять гипотезу Н₀, когда она неверна, обычно обозначают β.

Определение. Вероятность (1-β) не допустить ошибку 2-го рода, т.е. отвергнуть гипотезу Н₀, когда она неверна, называется мощностью (или функцией мощности) критерия.

Следует предпочесть ту критическую область, при которой мощность критерия будет наибольшей.

45. Построение теоретического закона распределения по опыт­ным данным. Понятие о критериях согласия.

Одной из важнейших задач матем-кой статистики является установление теоретического закона распределения случайной величины, характеризующей изучаемый признак по опытному (эмпирическому) распределению, представляющему вариационный ряд.