1) Распределение N (0;1) наз-ся станд-ным нормальным..Для стандартного распред-я плотность вер-ти равна: 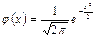 , а ф-я распред-я
, а ф-я распред-я 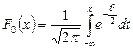 .
.
Ф-я Лапласа 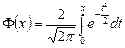 и ф-я распред-я НСВ Х с параметрами
и ф-я распред-я НСВ Х с параметрами 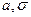 связаны соотнош-м:
связаны соотнош-м: 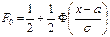 .
.
2)Получим формулу д/вычисления вер-ти попадания НСВ с параметрами 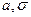 в задан. интервал(α;β) через стандарт-е распред-е
в задан. интервал(α;β) через стандарт-е распред-е 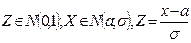 :
: 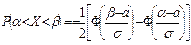
3) 3σ Вер-ть того, что НСВ отклоняется от своего мат.ожид-япо модулю меньше, чем ε>0, определяется формулой 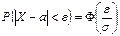 . Если положить
. Если положить 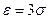 , то получим
, то получим 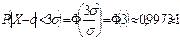 .
.
Отсюда вытекает, что среди 10000 значений НСВ в среднем только 27 выйдут за пределы интервала 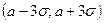 . Это означает, что практически среди небольшого числа значений Х нет таких, кот. выходят за пределы указанного интервала. Правило 3-х сигм часто применяется д/грубой оценки сигма:
. Это означает, что практически среди небольшого числа значений Х нет таких, кот. выходят за пределы указанного интервала. Правило 3-х сигм часто применяется д/грубой оценки сигма: 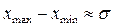 .
.
 2015-01-21
2015-01-21 1060
1060








