2015-01-21
813
Перевести восьмеричное число 745 в десятичную систему счисления:
.
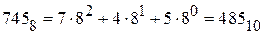Перевод в десятичный код может быть выполнен также по схеме Горнера. Процедура перевода следующая. Старший разряд исходного кода нужно умножить на основание переводимой системы счисления и полученное произведение сложить со следующим символом кода. Полученную сумму вновь умножить на основание и результат сложить со следующим символом и так продолжать до последнего (младшего) разряда кода. Для числа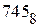 
указанные вычисления будут следующими:
.
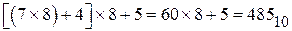Схема Горнера особенно удобна при переводе чисел из двоичной системы. Имеем: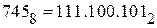 
. Переведем полученное двоичное число в десятичное:
Искомое десятичное число 485, т.е.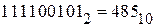 
.
3. Перевод чисел из любой недесятичной системы счисления в другую недесятичную систему выполняется в следующей последовательности:
– по методике, изложенной в п. 2, перевести исходный код в десятичный;
– по методике, изложенной в п. 1, перевести полученный десятичный код во вторую систему счисления.
Решение упрощается, если основания подлежащих переводу систем удовлетворяют условию (2.3), т.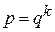е. 
, где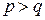 
, 
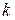– целое положительное число. При этом, если исходное число представлено в системе счисления с основанием 
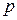, для получения его изображения в системе с основанием 
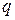достаточно каждый символ исходного кода представить 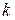-значным числом в системе счисления с основанием 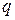. Примеры такого перевода приведены в п. 2.1.2 для чисел 
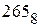и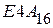 
. Если же исходное число представлено в системе счисления с основанием 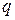, для получения его изображения в системе с основанием 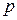нужно в последовательности символов исходного кода, начиная с младших разрядов, выделять группы по 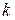знаков и каждой из этих групп поставить в соответствие число в системе счисления с основанием 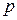. Если последняя группа окажется неполной, ее нужно дополнить нулями со стороны старших разрядов.
Примеры:
1) перевести двоичное число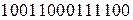 
в восьмеричную систему счисления (
):
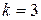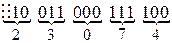
Получаем: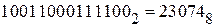 
;
2) перевести то же двоичное число в шестнадцатеричную систему счисления (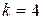
):
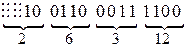
Получаем: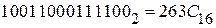 
.
Последние примеры показывают, что если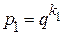 
, а 
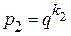, перевод чисел из системы счисления с основанием 
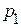в систему с основанием 
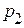и наоборот может выполняться через промежуточную систему счисления с основанием 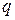. В частности, так можно осуществлять перевод чисел из восьмеричной системы в шестнадцатеричную и наоборот через двоичный код, т.е. сначала исходное число представляется в двоичном коде, затем полученная двоичная комбинация разбивается на группы, каждой из которых ставится число во второй системе счисления.
