1. Используя матричное представление построить контрольную матрицу для линейного кода (11,7).
Решение: линейные коды обозначают как 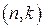 -коды, где
-коды, где 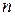 – значность кодовой комбинации, а
– значность кодовой комбинации, а 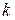 – число информационных символов в ней. Согласно заданию имеем:
– число информационных символов в ней. Согласно заданию имеем: 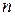 =11,
=11, 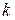 =7. Следовательно,
=7. Следовательно, 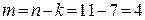 .
.
Строим порождающую матрицу:
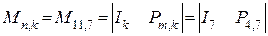
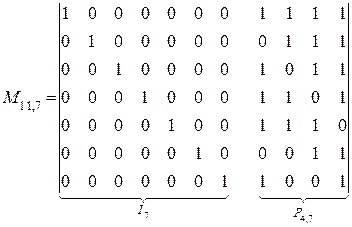
Контрольная матрица 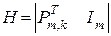
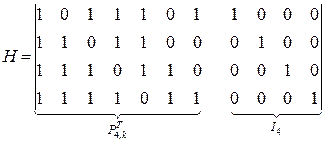
2. Построить контрольную матрицу линейного кода, ориентированного на исправление однократных ошибок. Требуемый объем кода Q=40.
Решение:
Определяем требуемое число информационных разрядов:
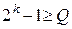 ,
, 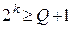 ,
, 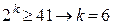
Так как код должен исправлять только одиночные ошибки, определение числа контрольных разрядов осуществляется в соответствии с выражением: 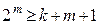 . Имеем:
. Имеем: 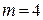 . Следовательно,
. Следовательно, 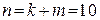 .
.
Строим порождающую матрицу 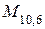 :
:
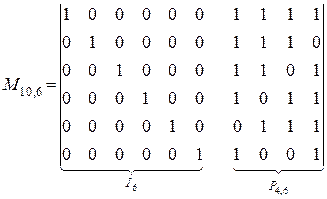
Контрольная матрица
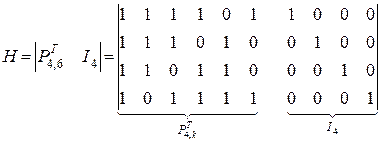
3. Из канала связи поступила комбинация линейного кода 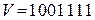 . Определить, какое число было передано. Контрольная матрица имеет вид:
. Определить, какое число было передано. Контрольная матрица имеет вид:
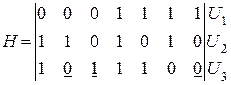
Решение:
Находим синдром ошибки
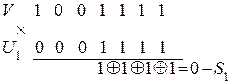
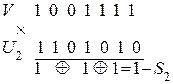
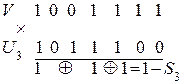
Итак, синдром ошибки 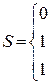 . Он совпадает с 1-м столбцом контрольной матрицы, следовательно, ошибка произошла в этом разряде. Исправляем этот разряд
. Он совпадает с 1-м столбцом контрольной матрицы, следовательно, ошибка произошла в этом разряде. Исправляем этот разряд 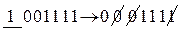 . По контрольной матрице определяем, что контрольными разрядами являются 2, 3 и 7 разряды. Следовательно, информационная часть имеет вид 0111=
. По контрольной матрице определяем, что контрольными разрядами являются 2, 3 и 7 разряды. Следовательно, информационная часть имеет вид 0111= 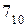 . Передавалось число
. Передавалось число 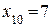 .
.
4. Закодировать линейным кодом число 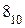 . Контрольная матрица имеет вид:
. Контрольная матрица имеет вид:
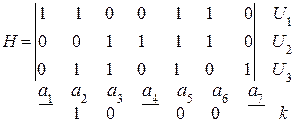
В формируемой комбинации контрольными разрядами будут 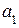 ,
, 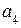 и
и 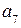 (соответствуют столбцам контрольной матрицы с одной 1). Составляем выражение для определения контрольных разрядов. Для того, чтобы формируемый кодовый вектор был ортогонален вектору
(соответствуют столбцам контрольной матрицы с одной 1). Составляем выражение для определения контрольных разрядов. Для того, чтобы формируемый кодовый вектор был ортогонален вектору 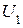 должно выполняться равенство:
должно выполняться равенство:
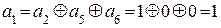
Ортогональность вектора 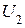 будет достигнута, если
будет достигнута, если 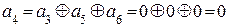 .
.
Ортогональность вектора 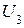 достигается, если
достигается, если 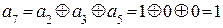 .
.
В окончательном виде 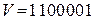 .
.
5. Закодировать циклическим кодом 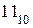 , образующий многочлен
, образующий многочлен 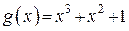 .
.
Разрешенные комбинации циклического кода формируются в соответствии с выражением: 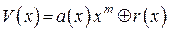 , где
, где 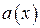 – многочлен, отображающий информационную часть; m – степень образующего многочлена, m =3;
– многочлен, отображающий информационную часть; m – степень образующего многочлена, m =3; 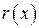 – остаток от деления многочлена
– остаток от деления многочлена 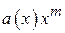 на
на  .
.
В виде кодовых векторов указанные многочлены имеют вид:
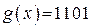 ;
; 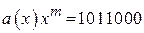 .
.
Находим остаток 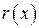 :
:
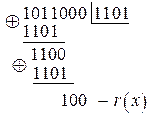
Итак, 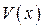 в виде КВ имеет вид:
в виде КВ имеет вид: 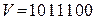 .
.
6. 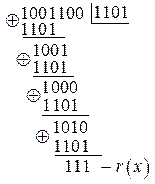 Из канала связи поступила комбинация ЦК 1001100,
Из канала связи поступила комбинация ЦК 1001100, 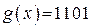 . Определить, какое число передавалось.
. Определить, какое число передавалось.
Находим остаток от деления принятого КВ на  :
:
Образующий многочлен  имеет 3 ненулевых члена, следовательно, кодовое расстояние кода, порождаемое этим многочленом,
имеет 3 ненулевых члена, следовательно, кодовое расстояние кода, порождаемое этим многочленом, 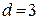 и код способен исправлять только однократные ошибки, т.е.
и код способен исправлять только однократные ошибки, т.е. 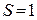 .
.
Имеем: вес остатка 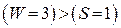 . Следовательно, принятую комбинацию нужно смещать циклически влево и вновь делить на
. Следовательно, принятую комбинацию нужно смещать циклически влево и вновь делить на  :
:
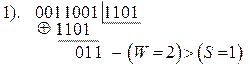
Требуется еще сдвиг:
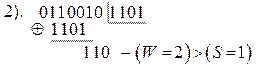
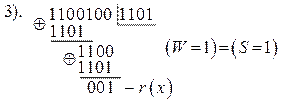
Складываем:
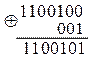 и сдвигаем в обратную сторону на 3 такта:
и сдвигаем в обратную сторону на 3 такта: 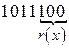 . Контрольные разряды отбрасываем. Получаем:
. Контрольные разряды отбрасываем. Получаем: 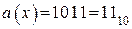 .
.
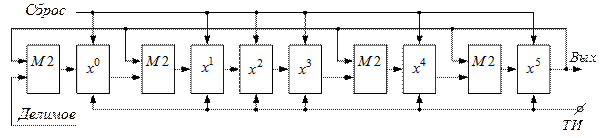
7. Построить схему делителя на образующий многочлен 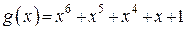
 2015-01-21
2015-01-21 2001
2001
