На рис.2.16 приведен общий вид дирижабля линзообразной формы.
Найдем проекции на оси связанной с дирижаблем системы координат 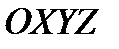 аэродинамических силы и момента, действующих на рули управления в приближении малости сил трения и пренебрежении интерференционными эффектами.
аэродинамических силы и момента, действующих на рули управления в приближении малости сил трения и пренебрежении интерференционными эффектами.
Свяжем с не отклоненным рулем управления систему координат 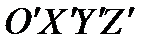 так, как показано на рис.2.13.
так, как показано на рис.2.13.
Рис.2.16
– К пояснению некоторых линейных и угловых размеров дирижабля линзообразной формы с двумя симметрично расположенными стабилизаторами и, следовательно, двумя рулями управления; система  связывается с главными осями центра масс эквивалентного дирижабля (см. выше); оси
связывается с главными осями центра масс эквивалентного дирижабля (см. выше); оси 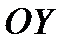 и
и 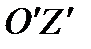 направлены по нормали к наблюдателю; руль изображен при
направлены по нормали к наблюдателю; руль изображен при 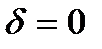
В нашем случае, как следует из рис.2.16, матрица направляющих косинусов 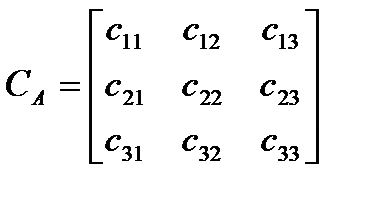 ,
,
характеризующих взаимную ориентацию этих двух систем координат, и вектор 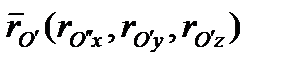 , характеризующий смещение начала координат связанной с не отклоненным рулем системы относительно начала координат дирижабля в целом, соответственно равны:
, характеризующий смещение начала координат связанной с не отклоненным рулем системы относительно начала координат дирижабля в целом, соответственно равны:
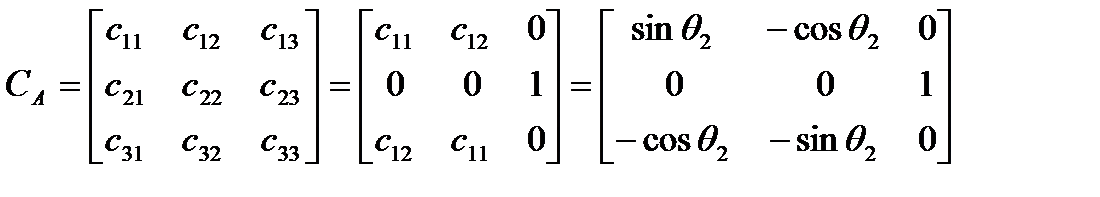 ,
, 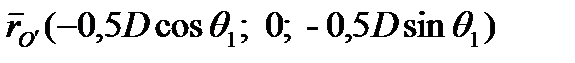 ,
,
(2.102)
Положение центра масс пластины не отклоненного руля характеризуется в связанной с рулем системе координатами 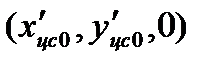 . При отклонении руля на угол
. При отклонении руля на угол 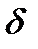 положение смещенного центра масс пластины характеризуется вектором
положение смещенного центра масс пластины характеризуется вектором 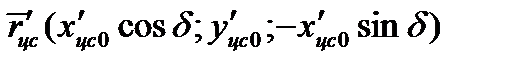 .
.
Тогда в системе координат, связанной с дирижаблем, компоненты радиус-вектора, описывающего положение центра масс руля при отклонении его на угол 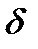 , определяются с помощью матрицы однородных преобразований
, определяются с помощью матрицы однородных преобразований
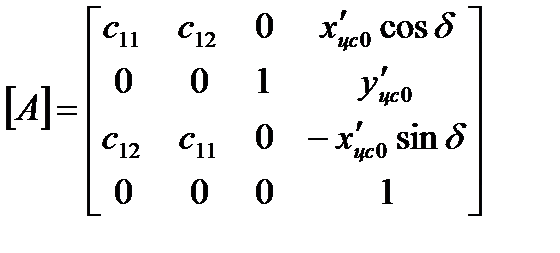 следующим образом:
следующим образом:
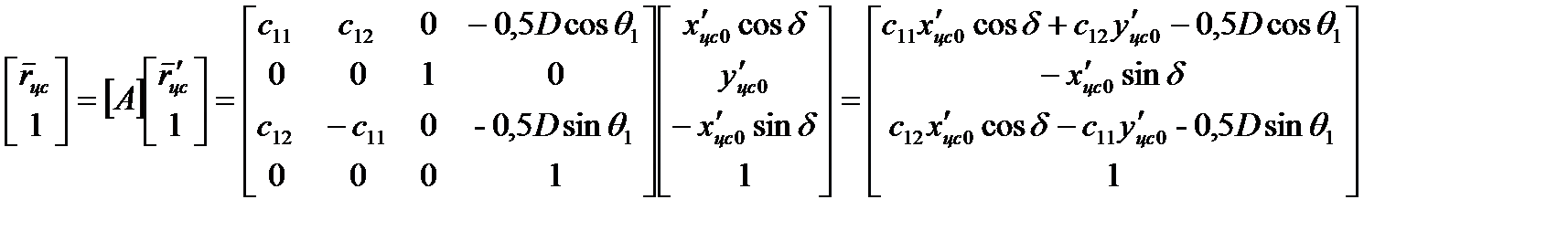 .
.
(2.103)
Компоненты вектора аэродинамической силы от действия левого руля управления в системе координат  определяются по формуле (2.89):
определяются по формуле (2.89):
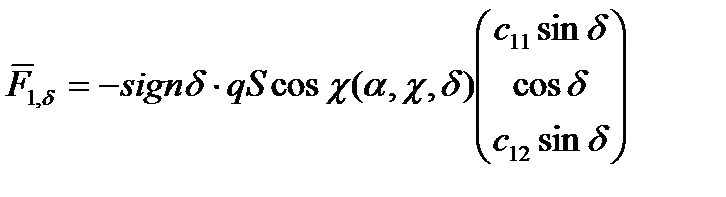 , (2.104)
, (2.104)
где 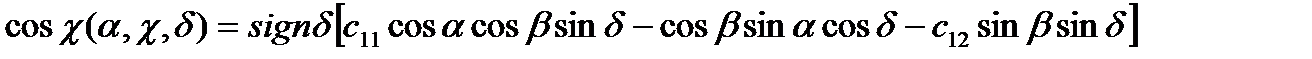 .
.
Напомним, что 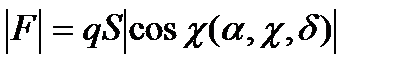 - модуль вектора силы в указанном приближении,
- модуль вектора силы в указанном приближении, 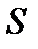 - площадь руля,
- площадь руля, 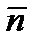 - та нормаль (из двух) к пластине, которая в системе
- та нормаль (из двух) к пластине, которая в системе 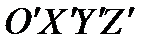 характеризуется координатами
характеризуется координатами 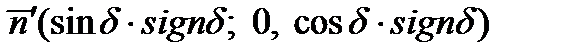 (см. рис.2.13 и рис.2.16).
(см. рис.2.13 и рис.2.16).
Подставляя в (2.104) значения коэффициентов 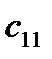 ,
, 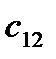 матрицы поворота
матрицы поворота 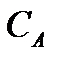 , получим:
, получим:
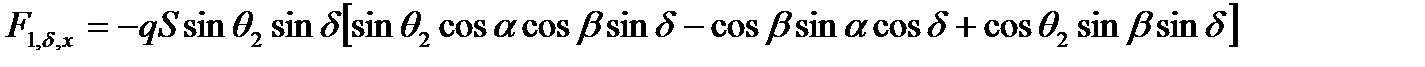 ,
,
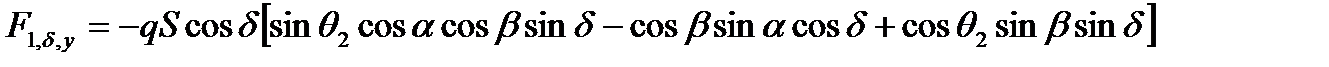 ,
,
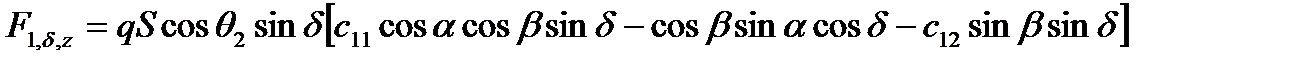 . (2.105)
. (2.105)
Для расчета составляющих момента аэродинамической силы 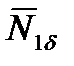 используем формулы (2.91).
используем формулы (2.91).
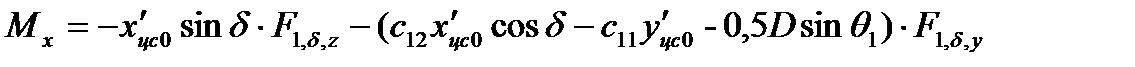 ,
, 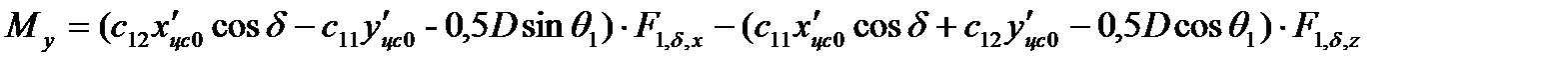 ,
,
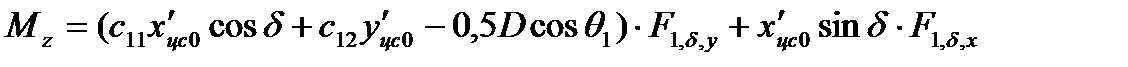 , (2.106)
, (2.106)
 2015-01-21
2015-01-21 409
409








