Пусть задача линейного программирования записана в каноническом виде в векторной записи
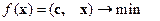 , (6.16)
, (6.16)
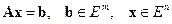 , (6.17)
, (6.17)
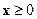 . (6.18)
. (6.18)
Считаем, что матрица А размера m × n, m < n, имеет ранг, равный m. Тогда система уравнений (6.17) совместна и имеет бесчисленное множество решений.
Из курса линейной алгебры известна процедура получения общего решения системы (6.17) методом последовательных исключений Жордана – Гаусса.
Выберем какой-нибудь базисный минор (т.е. минор порядка m, отличный от нуля) матрицы А. Для определенности будем считать, что он соответствует первым m столбцам матрицы А. Назовем переменные x 1, …, xm − базисными, а остальные переменные xm+ 1, …, xn − свободными. При выборе базисных переменных на первом шаге достаточно воспользоваться следующим правилом: в качестве базисных переменных следует выбрать (если возможно) такие m переменных, каждая из которых входит только в одно из m уравнений системы ограничений, при этом нет таких уравнений системы, в которые не входит ни одна из этих переменных.
Выполним элементарные преобразования строк расширенной матрицы системы (А / b) так, чтобы в первых m столбцах располагалась единичная матрица. В результате получим следующую систему уравнений, эквивалентную исходной:
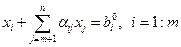 . (6.19)
. (6.19)
Тогда общее решение системы уравнений (6.17) запишется следующим образом:
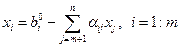 , (6.20)
, (6.20)
где свободные переменные 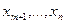 могут принимать произвольные значения.
могут принимать произвольные значения.
Положив их равными нулю, получим частное решение:
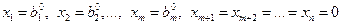
или
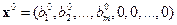 , (6.21)
, (6.21)
которое называется базисным решением этой системы.
Если все компоненты базисного решения (6.21) удовлетворяют условию неотрицательности, т.е. если 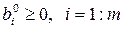 , то такое решение называют допустимым базисным решением системы (6.17) или угловой точкой допустимого множества Е задачи линейного программирования (6.16)…(6.18). Если среди неотрицательных чисел
, то такое решение называют допустимым базисным решением системы (6.17) или угловой точкой допустимого множества Е задачи линейного программирования (6.16)…(6.18). Если среди неотрицательных чисел 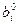 в (6.21) есть равные нулю (
в (6.21) есть равные нулю (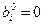 ), то допустимое базисное решение называется вырожденным (вырожденной угловой точкой), а соответствующая задача линейного программирования также называется вырожденной, а в противном случае (
), то допустимое базисное решение называется вырожденным (вырожденной угловой точкой), а соответствующая задача линейного программирования также называется вырожденной, а в противном случае (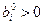 ) – невырожденной.
) – невырожденной.
В основе симплекс – метода лежит следующий факт:
Если задача линейного программирования (6.16)…(6.18) разрешима, то минимум целевой функции f (x) из (6.16) достигается хотя бы в одной из угловых точек допустимого множества X этой задачи.
Каждому выбору m базисных переменных системы (6.17) соответствует свое базисное решение. Поэтому число базисных решений (угловых точек) равно числу всевозможных базисных миноров матрицы А, т.е. не превосходит 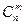 .
.
Предположим что задача линейного программирования (6.16)…(6.18) является невырожденной, а базисное решение (6.21) – допустимым.
Выразим целевую функцию задачи (6.16)…(6.17) через свободные переменные решения (6.21). Для этого подставим выражения базисных переменных через свободные из (6.20) в равенство (6.16):
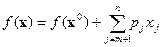 , (6.22)
, (6.22)
где 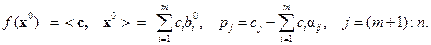
Величина pj называется относительной оценкой небазисных переменных (xm +1,…, xn). Если pj < 0, то можно добиться уменьшения значения целевой функции f, вводя переменную xn в базис.
Для получения промежуточного допустимого базисного решения симплекс–метод превращает одну из базисных переменных в небазисную и вводит одну из небазисных переменных в базис. Необходимо выбрать базисную и небазисную переменные так, чтобы замена одной из них на другую давала максимальное приращение целевой функции.
В любом базисном решении базисные переменные положительны, а небазисные равны нулю. Следовательно, превращение небазисной переменной в базисную приводит к увеличению её значения от нуля до некоторой положительной величины. Вводимая в базис переменная должна давать улучшение значения f. Для выбора вводимой в базис переменной следует присвоить небазисной переменной значение, равное единице, и вычислить изменение целевой функции.
Задача линейного программирования
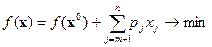 , (6.23)
, (6.23)
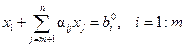 , (6.24)
, (6.24)
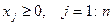 (6.25)
(6.25)
имеет канонический вид, соответствующий допустимому базисному решению 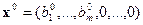 . Ее можно записать компактно, с помощью, так называемой симплекс-таблицы (табл. 6.3).
. Ее можно записать компактно, с помощью, так называемой симплекс-таблицы (табл. 6.3).
Таблица 6.3
Симплекс-таблица
| xm+ 1 … xj … xn | ||
| x 1 . . xi . . xm | a 1 m+ 1 … a 1 j … a 1 n . . aim+ 1 … aij … ain . . amm+ 1 … amj … amn | 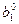 .
..
.
..
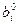 .
.
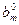
|
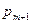 … … 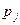 … … 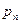
| 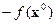
|
Строке с номером i таблицы 6.3 соответствует i -ое уравнение системы (6.24): 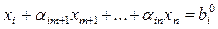 , а в последней строке записаны коэффициенты
, а в последней строке записаны коэффициенты 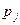 из выражения (6.23) и значение f (x 0), взятое со знаком минус.
из выражения (6.23) и значение f (x 0), взятое со знаком минус.
Пример 6.7. Записать одну из симплекс-таблиц для задачи:
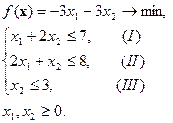
Для того чтобы перейти к каноническому виду рассматриваемой задачи, прибавим к левым частям соответствующих ограничений-неравенств дополнительные переменные 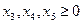 :
:
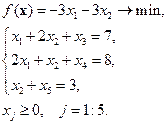 (6.26)
(6.26)
В качестве базисных переменных удобно выбрать x 3, x 4 и x 5, тогда переменные x 1и x 2будут свободными. Выпишем общее решение системы уравнений из (6.26):
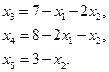
Полагая свободные переменные x 1и x 2 равными нулю, получаем базисное решение x 0 = (0;0;7;8;3). Очевидно, оно является допустимым базисным решением или угловой точкой множества X. Так как целевая функция задачи (6.26) зависит лишь от свободных переменных, то выражения (6.26) представляют собой канонический вид задачи линейного программирования, соответствующий допустимому базисному решению x 0. Таким образом, искомая симплекс-таблица имеет вид (табл. 6.4):
Таблица 6.4
Симплекс-таблица задачи 6.9
| x 1 | x 2 | ||
| x 3 | |||
| x 4 | |||
| x 5 | |||
| -3 | -3 |
 2015-02-04
2015-02-04 557
557








