Для решения задач максимизации можно использовать два подхода.
Подход1. Преобразование задачи максимизации в эквивалентную задачу минимизации путём умножения целевой функции на –1 и последующего применения симплекс–метода к задаче минимизации.
Подход 2. Как показано выше, относительные оценки в строке pj представляют изменение целевой функции f при уменьшении небазисной переменной на единицу. Отрицательный коэффициент в строке pj указывает на уменьшение f при увеличении соответствующей небазисной переменной.
Следовательно, для задач максимизации в базис должны вводится небазисные переменные xj с положительными pj, поскольку они улучшают целевую функцию. Если все коэффициенты в строке pj отрицательные или равны нулю, текущее решение оптимальное.
Пример 6.9. Решить симплекс – методом задачу:
f (x) = 2 х 1+3 х 2→max
при ограничениях
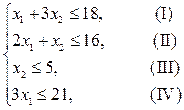
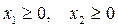 .
.
Решение. С помощью дополнительных неотрицательных переменных перейдем к системе уравнений. В данном случае все дополнительные переменные вводятся со знаком «+», так как все неравенства имеют вид «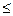 ».
».
Получим систему ограничений в виде:

И т е р а ц и я 1.
Полагая в равенствах (6.37) свободные переменные x 1, x 2 равными нулю, находим 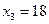 ,
, 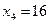 ,
, 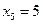 ,
, 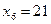 , т.е. базисное решение х 0 = (0;0;18;16;5;21). Так как все базисные переменные в х 0 положительны, данное базисное решение является допустимым (угловой точкой) и невырожденным. Используя подход 1, перейдем к задаче минимизации
, т.е. базисное решение х 0 = (0;0;18;16;5;21). Так как все базисные переменные в х 0 положительны, данное базисное решение является допустимым (угловой точкой) и невырожденным. Используя подход 1, перейдем к задаче минимизации
f (x) = − 2 x 1 − 3 x 2 → min. (6.36)
С помощью равенств (6.35) и (6.36) составляем симплекс – таблицу, соответствующую угловой точке х 0:
Таблица 6.9
Начальная симплекс-таблица
| Базис | Переменные | Свободный член | Оценочное отношение | |
| x 1 | x 2 | |||
x 3 x 4  x 5 x 6 x 5 x 6 | 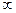 | |||
 f (x) f (x) | -2 | -3 |
В соответствии с п.4 алгоритма проверяем критерий оптимальности. В последней строке имеются отрицательные коэффициенты. Выберем из них наибольший по модулю (-3); второй столбец разрешающий, переменная x 2 перейдет в основные (этот столбец отмечен стрелкой). В соответствии с п.5 находим оценочные отношения и 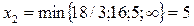 . Третья строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит опорный элемент
. Третья строка является разрешающей (отмечена горизонтальной стрелкой). На пересечении разрешающих строки и столбца стоит опорный элемент 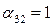 (обведен рамкой).
(обведен рамкой).
И т е р а ц и я 2. Строим таблицу по правилам п.6 алгоритма (табл. 6.10). В новом базисе основные переменные: 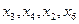 .
.
Критерий оптимальности вновь не найден. Теперь первый столбец разрешающий; x 1 – переход в основные, 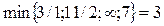 ; первая строка разрешающая,
; первая строка разрешающая, 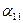 - опорный элемент.
- опорный элемент.
Таблица 6.10
Симплекс-таблица для угловой точки х 1
| Базис | Переменные | Свободный член | Оценочное отношение | |
| x 1 | x 5 | |||
 x 3 x 4 x 2 x 6 x 3 x 4 x 2 x 6 | -3 -1 | 11/2 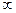 | ||
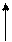 f (x) f (x) | -2 |
И т е р а ц и я 3. Новая симплексная таблица примет вид (табл. 6.11).
Таблица 6.11
Симплекс-таблица для угловой точки х 2
| Базис | Переменные | Свободный член | Оценочное отношение | |
| x 3 | x 5 | |||
x 1  x 4 x 2 x 6 x 4 x 2 x 6 | -2 -3 | -3 | 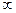 12/9 12/9 | |
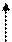 f (x) f (x) | -3 |
И на этот раз критерий оптимальности не выполнен; второй столбец и вторая строка – разрешающие, 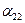 - опорный элемент.
- опорный элемент.
И т е р а ц и я 4. Переходим к таблице 6.12.
Таблица 6.12
Симплекс-таблица для угловой точки х 3
| Базис | Переменные | Свободный член | |
| x 3 | x 4 | ||
| x 1 x 5 x 2 x 6 | -1/5 -2/5 2/5 3/5 | 3/5 1/5 -1/5 -9/5 | |
| f (x) | 4/5 | 3/5 |
Критерий оптимальности выполнен, значит f * = f (х *) = 24, оптимальное базисное решение х * = (6,4,0,0,1,3).
Графическое решение задачи представлено на рис. 6.10, откуда видно, что х * = (6;4), и f * = f (х *) = 24.
f (x) = 2 х 1 + 3 х2 →max
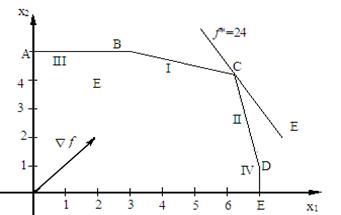
Рис. 6.10. Графическое решение задачи 6.19
 2015-02-04
2015-02-04 3120
3120








