Положения: При использовании теоремы Гаусса для расчета электрических полей нужно учитывать, что:
1) рассчитать можно только поле, которое обладает специальной симметрией (чаще всего плоской, цилиндрической или сферической).
2) симметрия и конфигурация поля должны быть такими, чтобы можно было найти достаточно простую замкнутую поверхность S (называемую гауссовой поверхностью), такую, чтобы отдельные ее части Si были параллельны вектору 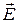 (тогда
(тогда 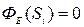 ) или отдельные ее части Sj были перпендикулярны
) или отдельные ее части Sj были перпендикулярны 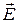 и напряженность на них была постоянна по модулю (тогда
и напряженность на них была постоянна по модулю (тогда 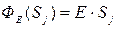 ).
).
Если этого нет, задачу о нахождении поля приходится решать помощью метода непосредственного интегрирования или с помощью других методов, с которыми мы ознакомимся ниже.
Рассчитаем:
1) поле бесконечной заряж. равном. плоскости
Дано:
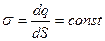
 |
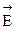 -?
-?
Из симметрии задачи вектор 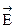 ^ плоскости и в симметр. отн. плоскости точках одинаков. по модулю и противоп. по направлению (Рис. 11). Гауссова поверхность – цилиндр. Тогда поток вектора напр. находится как сумма потоков через основания и боковую поверхность.
^ плоскости и в симметр. отн. плоскости точках одинаков. по модулю и противоп. по направлению (Рис. 11). Гауссова поверхность – цилиндр. Тогда поток вектора напр. находится как сумма потоков через основания и боковую поверхность.
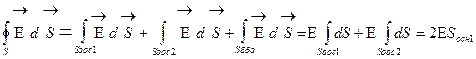 Þ
Þ
Þ теор. Г. 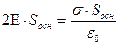 Þ
Þ 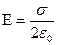 напр. равном. заряж. плоскости
напр. равном. заряж. плоскости
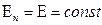
 2015-02-24
2015-02-24 539
539








