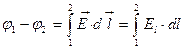
интеграл может быть взят по любому пути соединяющему (1) и (2)
если (1) и (2) лежат на силовой линии, то в качестве линии, соединяющей (1) и (2) нужно взять силовую.
Понятие потенциала можно ввести для любого потенциального векторного поля. (потенциал гравит. силы, потенциал скорости и т.д.)
Потенциал Часто в качестве точки (2) выбирают точку, потенциал которой по определению = 0.
φ2 = 0
В теории – такая точка бесконечно удаленная: 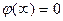 .
.
Замечание Это можно сделать лишь тогда, если заряды располагаются в ограниченной области пространства и их нет на бесконечности.
На практике 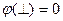 -- потенциал земли = 0.
-- потенциал земли = 0.
Потенциал электростатического поля в т. B(x,y,z) назыв.
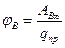 потенциал какой-то точки, когда в ¥ = 0.
потенциал какой-то точки, когда в ¥ = 0.
Расчетная формула: 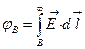
Потенциал поля точечного заряда
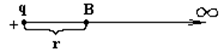 Рис. 18 Рис. 18 |
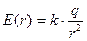
Путь из точки B в ∞ может быть любым, т.к. поле потенциально. Наиболее удобно выбрать L вдоль радиуса вектора, проведенного из точечного заряда
=> dl = dr;
El = Er = E(r); => 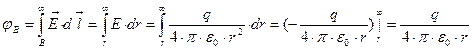 =>
=>
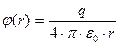 формула имеет смысл для r ≠ 0, т.к. r →∞.
формула имеет смысл для r ≠ 0, т.к. r →∞.
Т.к. поле точечного заряда фундаментально => для нахождения потенциала поля системы зарядов нужно применить принцип суперпозиций:
потенциал поля системы точечных зарядов равен сумме потенциалов, издаваемых в рассматриваемой точке каждым из зарядов.
а) потенциал поля системы точечных зарядов:
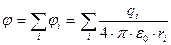
б) потенциал поля непрерывного распределения зарядов:
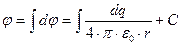
где dq = ρ∙dV -- при объемном распределении заряда,
dq = σ∙dS -- при поверхностном
dq = λ∙dl -- при линейном.
Применение формулы поля точечного заряда и принципа суперпозиций составляет основу метода непосредственного интегрирования и позволяет рассчитать потенциал поля новой системы зарядов. Графически потенциал изображается в виде эквипотенциальных поверхностей и линий на которой он принимает постоянное значение = const.
Примеры расчета потенциала
(I) Равномерно заряженная бесконечная нить. (Рис. 19)
Дано: 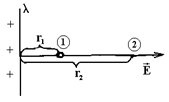 l;
l;
_____________
j (r1)-j(r2) -?
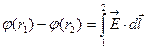
Т.к. поле нити имеет осевую симметрию и 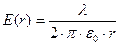 => в качестве линии L, соединяющей 1 и 2 берем отрезок силовой линии, соединяющей точки 1 и 2. =>
=> в качестве линии L, соединяющей 1 и 2 берем отрезок силовой линии, соединяющей точки 1 и 2. => 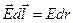 =>
=>
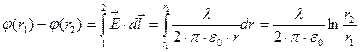
 2015-02-24
2015-02-24 1254
1254








