Векторным произведением векторов 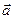 и
и 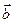 называется вектор
называется вектор 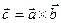 , определяемый следующим образом:
, определяемый следующим образом:
1) 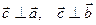
2) 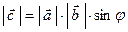
3) векторы 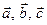 образуют правую тройку.
образуют правую тройку.
С помощью векторного произведения можно находить:
1) Вектор, перпендикулярный плоскости, которой параллельны векторы 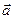 и
и 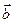
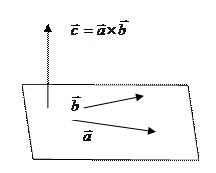
2) Площадь параллелограмма и треугольника, построенного на векторах 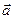 и
и 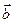 соответст-
соответст-
венно по формулам:
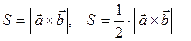
Вычисляется векторное произведение с помощью определителя:
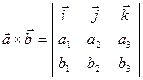
Пример. Найти векторное произведение векторов 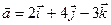 и
и 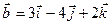
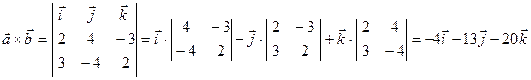
Проверим вычисления. Так как 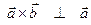 и
и 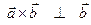 , то надо убедиться, что скалярные произведения равны нулю:
, то надо убедиться, что скалярные произведения равны нулю:
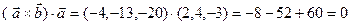
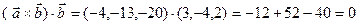
Пример. Найти площадь треугольника с вершинами 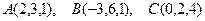
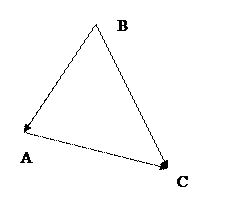
Найдем координаты векторов 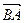 ,
, 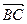 :
: 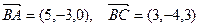 . Затем находим векторное произведение:
. Затем находим векторное произведение:
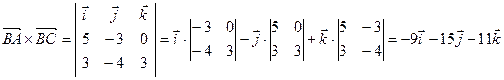
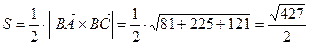 .
.
 2015-02-04
2015-02-04 604
604








