1.
Рассмотрим прямоугольную декартову систему координат на плоскости. Единичный вектор оси 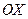 обозначим
обозначим 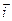 , единичный вектор оси
, единичный вектор оси 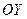 обозначим
обозначим 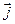 . Таким образом,
. Таким образом, 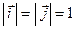 и
и 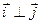 . Говорят, что векторы
. Говорят, что векторы 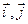 образуют ортонормированный базис на плоскости.
образуют ортонормированный базис на плоскости.
Любой вектор 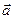 можно выразить через вектора
можно выразить через вектора 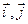 , то есть представить в виде
, то есть представить в виде 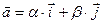 . Это представление называется разложением вектора
. Это представление называется разложением вектора 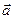 по базису
по базису 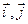 . Числа
. Числа 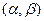 называются координатами вектора
называются координатами вектора 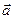 в базисе
в базисе 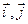 .
.
|
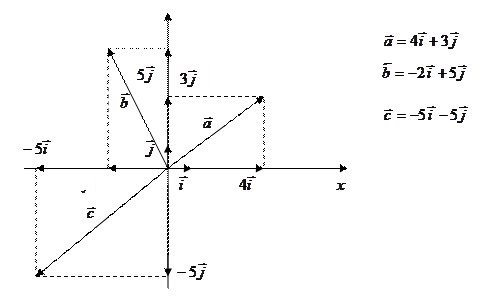
Любые два непараллельных вектора 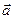 и
и 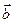 образуют базис на плоскости и любой третий вектор
образуют базис на плоскости и любой третий вектор 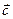 может быть разложен по этому базису, то есть представлен в виде
может быть разложен по этому базису, то есть представлен в виде 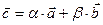 .Числа
.Числа 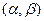 называются координатами вектора
называются координатами вектора 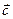 в базисе
в базисе 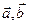 .
.
Пример. Проверить, что векторы 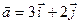 и
и 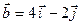 образуют базис и разложить вектор
образуют базис и разложить вектор 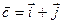 по этому базису.
по этому базису.
Векторы параллельны, если их координаты пропорциональны:
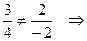 координаты не пропорциональны, значит, векторы
координаты не пропорциональны, значит, векторы 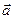 и
и 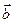 непараллельны, то есть образуют базис.
непараллельны, то есть образуют базис.
Найдем числа 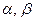 такие, что
такие, что 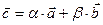 .
.
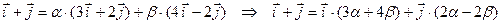
Векторы слева и справа равны, значит, равны их координаты:
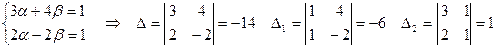
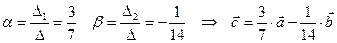
- Скалярное произведение векторов.
Скалярным произведением векторов 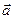 и
и 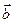 называется число
называется число
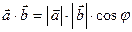 .
.
Здесь 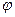 - угол между этими векторами,
- угол между этими векторами, 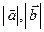 - длины векторов.
- длины векторов.
Скалярное произведение позволяет:
- Находить угол между векторами по формуле
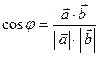
- Находить проекцию вектора
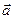 на вектор
на вектор 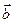 по формуле
по формуле
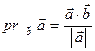
- Проверять, будут ли векторы перпендикулярны, так как
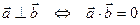
Пусть в ортонормированном базисе заданы векторы 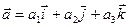 и
и 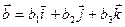 .
.
Тогда длина (модуль) вектора находится по формуле 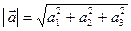 , а скалярное произведение
, а скалярное произведение 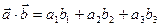
 2015-02-04
2015-02-04 1467
1467