В форме сил

Приведем все массы звеньев механизма к приведенной массе, расположенной в точке приведения ведущего звена, а все силы и моменты к приведенной силе, приложенной в этой же точке. Тогда кинетическая энергия механизма будет

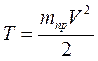
А ее производная

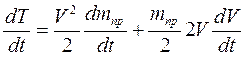
Учитывая, что значение приведенной массы зависит от дуговой координаты точки приведения можно записать

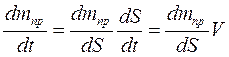
Где 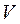- скорость точки приведения.

Тогда

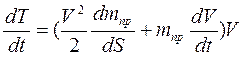
Мощность всех сил будет

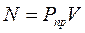
Подставляя эти выражения в формулу изменения кинетической энергии (6.23) получим уравнение движения механизма в форме сил

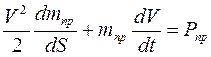(6.24)

Если приведенная масса в процессе движения не изменяется, т.е. 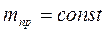, то это уравнение приобретает более простой вид

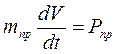
Который формально соответствует уравнению движения материальной точки массой 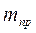расположенной в точке приведения. Таким образом, движение любого сложного механизма сводится к исследованию движения одной материальной точки, что значительно упрощает задачу исследования.