Так как 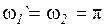 , поэтому траектория точки будет эллипс. Исключив t, получим:
, поэтому траектория точки будет эллипс. Исключив t, получим:
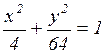 , (1)
, (1)
Затем, сравнивая с уравнением эллипса 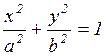 , находим:
, находим: 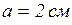 и
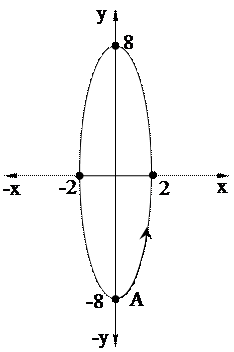
и 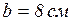 .
.
Теперь находим направление точки, в момент времени 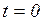 ,
, 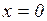 , а
, а 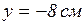 . Следовательно, точка находится в положении А. При возрастании t увеличивается х, значит точка движения против часовой стрелки.
. Следовательно, точка находится в положении А. При возрастании t увеличивается х, значит точка движения против часовой стрелки.
Определим значение скорости и ускорения точки. Скорость равна векторной сумме скоростей 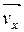 и
и 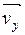 . Так как они взаимно перпендикулярны, поэтому получим:
. Так как они взаимно перпендикулярны, поэтому получим:
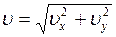 (2)
(2)
Аналогично, получим для ускорения:
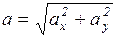 (3)
(3)
Взяв первую и вторую производную, получим:
 (4)
(4)
 (5)
(5)
Поставив (4) в (2) и (5) в (3), найдем:
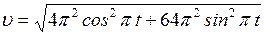 (6)
(6)
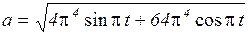 (7)
(7)
Взяв 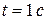 и выполнив вычисление, получим:
и выполнив вычисление, получим:
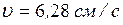 ,
, 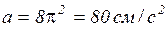
 2015-02-24
2015-02-24 723
723








