Закон Ампера. На элемент проводника  с током I, помещённый в магнитное поле с индукцией
с током I, помещённый в магнитное поле с индукцией 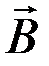 действует сила
действует сила 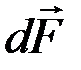 (
(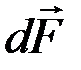 – сила Ампера):
– сила Ампера): 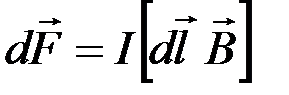 .
.
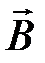
|
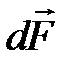
|

|
|
| Рис. 13 |
|
| I |
| I |
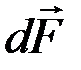 :
: 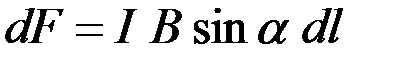 ,
,
где 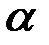 – угол между векторами
– угол между векторами  и
и 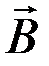 .
.
Направление вектора 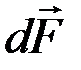 можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера (рис. 13, сила
можно определить по правилу левой руки: если силовые линии входят в ладонь, а четыре вытянутых пальца располагаются по току, то отведённый большой палец укажет направление силы Ампера (рис. 13, сила 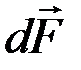 перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).
Сила Лоренца. На заряд q, движущийся со скоростью 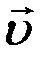 в магнитном поле с индукцией
в магнитном поле с индукцией 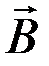 , действует сила
, действует сила 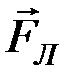 (
(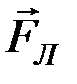 – сила Лоренца):
– сила Лоренца):  .
.
Модуль вектора 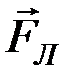 :
: 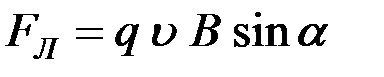 ,
,
где α – угол между векторами 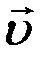 и
и 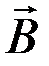 .
.
| Рис. 14 |
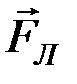 может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила
может быть определено по правилу левой руки для движущихся положительных зарядов и по правилу правой руки для движущихся отрицательных зарядов: если силовые линии магнитного поля входят в ладонь, а четыре вытянутых пальца располагаются по скорости движения частицы, то отведённый большой палец укажет направление силы Лоренца (рис.14, сила 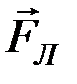 перпендикулярна плоскости рисунка).
перпендикулярна плоскости рисунка).|
|
|
Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля
Поток вектора магнитной индукции 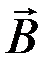 ( или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB
( или магнитный поток) через произвольную площадку S характеризуется числом силовых линий магнитного поля, пронизывающих данную площадку S. Если площадка S расположенаперпендикулярно силовым линиям магнитного поля (рис. 15), то поток ФB
вектора индукции  через данную площадку S:
через данную площадку S: 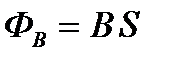 .
.
| S |

|
| S |
|
| α |

|
Рис. 15 Рис. 16
Если площадка S расположена неперпендикулярно силовым линиям магнитного поля (рис. 16), то поток ФB вектора индукции  через данную площадку S:
через данную площадку S:
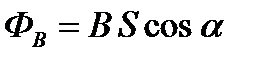 ,
,
где α – угол между векторами  и нормали
и нормали 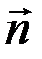 к площадке S.
к площадке S.
| dS |
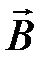
|
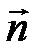
|
| α |
| S |

|
| Рис. 17 |
 через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 17)иопределить элементарный поток
через произвольную поверхность S, необходиморазбить эту поверхность на элементарные площадки dS (рис. 17)иопределить элементарный поток 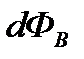 вектора
вектора  через каждую площадку dS по формуле:
через каждую площадку dS по формуле: 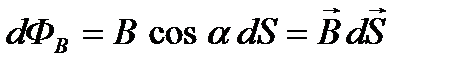 ,
,
где α – угол между векторами  и нормали
и нормали 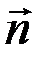 к данной площадке dS;
к данной площадке dS;
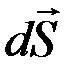 – вектор, равный по величине площади площадки dS и направленный по вектору нормали
– вектор, равный по величине площади площадки dS и направленный по вектору нормали 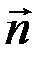 к данной площадке dS.
к данной площадке dS.
Тогда поток вектора  через произвольную поверхность S равен алгебраической сумме элементарных потоков
через произвольную поверхность S равен алгебраической сумме элементарных потоков 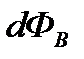 через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
через все элементарные площадки dS, на которые разбита поверхность S, что приводит к интегрированию:
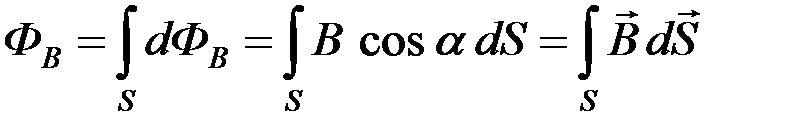 .
.
Теорема Гаусса для магнитного поля
| S |
| Рис. 18 |
|
| α |
| dS |

|
|
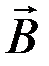 магнитного поля через эту поверхность S можно рассчитать по формуле:
магнитного поля через эту поверхность S можно рассчитать по формуле:
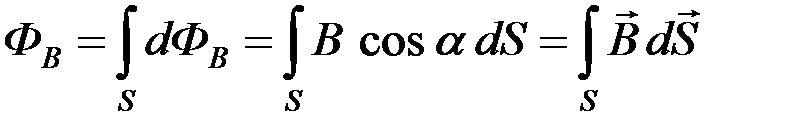 .
.
С другой стороны, число линий магнитной индукции, входящих внутрь объема, ограниченного этой замкнутой поверхностью, равно числу линий, выходящих из этого объема (рис. 18). Поэтому, с учетом того, что поток вектора индукции  магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора индукции
магнитного поля считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, суммарный поток ФB вектора индукции  через произвольную замкнутую поверхность S равен нулю, то есть:
через произвольную замкнутую поверхность S равен нулю, то есть:
|
|
|
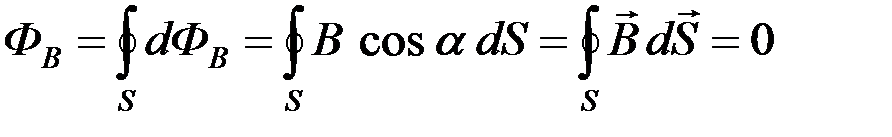 ,
,
что составляет формулировку теоремы Гаусса для магнитного поля.
Тема. 6. Явление электромагнитной индукции. Закон Фарадея
Явление возникновения электрического тока в замкнутом проводящем контуре в результате изменения магнитного потока, пронизывающего этот контур, называется явлением электромагнитной индукции. Возникновение индукционного электрического тока в контуре указывает на наличие в этом контуре электродвижущей силы, называемой электродвижущей силой (ЭДС) электромагнитной индукции.
Согласно закону Фарадея, величина ЭДС электромагнитной индукции 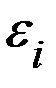 определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
определяется только скоростью изменения магнитного потока, пронизывающего проводящий контур, а именно:
величина ЭДС электромагнитной индукции  прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
прямо пропорциональна скорости изменения магнитного потока, пронизывающего проводящий контур:
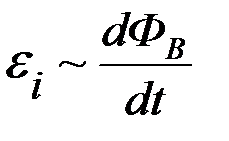 (закон Фарадея).
(закон Фарадея).
Направление индукционного тока в контуре определяется по правилу Ленца: индукционный ток в контуре всегда имеет такое направление, что создаваемое этим током магнитное поле препятствует изменению магнитного потока, вызвавшему этот индукционный ток.
Закон Фарадея с учетом правила Ленца можно сформулировать следующим образом: величина ЭДС электромагнитной индукции 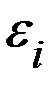 в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
в контуре численно равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную этим контуром, то есть:
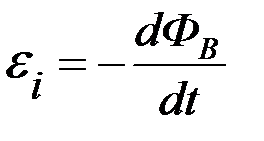 (закон Фарадея с учетом правила Ленца).
(закон Фарадея с учетом правила Ленца).
Тема 7. Циркуляция вектора магнитной индукции 
Циркуляцией вектора магнитной индукции  по произвольному замкнутому контуру L называется интеграл:
по произвольному замкнутому контуру L называется интеграл:
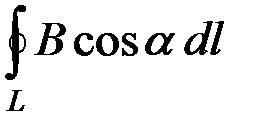 .
.
Для того, чтобы найти циркуляцию вектора магнитной индукции  по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы
по произвольному замкнутому контуру L, необходимо выбрать направление обхода контура, разбить этот контур L на элементы 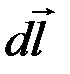 , для каждого элемента
, для каждого элемента 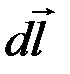 рассчитать величину
рассчитать величину 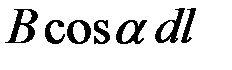 (a – угол между векторами
(a – угол между векторами  и
и 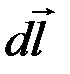 ), а затем все эти величины сложить, что приводит к искомому интегралу.
), а затем все эти величины сложить, что приводит к искомому интегралу.
Однако циркуляцию вектора  по произвольному замкнутому контуру L можно рассчитать, используя теорему о циркуляции вектора
по произвольному замкнутому контуру L можно рассчитать, используя теорему о циркуляции вектора  .
.
Теорема о циркуляции вектора  : циркуляция вектора
: циркуляция вектора  по произвольному замкнутому контуру L равна произведению магнитной постоянной m 0 на алгебраическую сумму токов, охватываемых этим контуром L:
по произвольному замкнутому контуру L равна произведению магнитной постоянной m 0 на алгебраическую сумму токов, охватываемых этим контуром L:
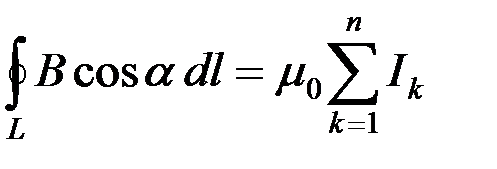 ,
,
где n – число проводников с токами, охватываемых контуром L. Положительным считается ток, направление которого образует с направлением обхода по контуру правовинтовую систему; ток противоположного направления считается отрицательным.
Величина 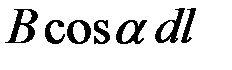 , где a – угол между векторами
, где a – угол между векторами  и
и 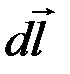 может быть записана в виде скалярного произведения векторов
может быть записана в виде скалярного произведения векторов  и
и 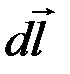 , то есть, как
, то есть, как 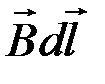 , а полученное соотношение для циркуляции вектора
, а полученное соотношение для циркуляции вектора  примет вид:
примет вид:
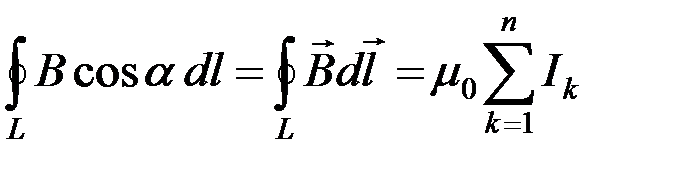 .
.
Магнитное поле претерпевает изменения при переходе из одного вещества в другое, что определяется магнитными свойствами вещества, которые характеризуются величиной магнитной проницаемости среды (m).
Кроме вектораиндукции  магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и вектор напряженности
магнитного поля, учитывающего магнитные свойства вещества, для описания магнитного поля введен также и вектор напряженности 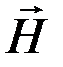 магнитного поля, причем для однородной изотропной среды вектор магнитной индукции
магнитного поля, причем для однородной изотропной среды вектор магнитной индукции  связан с вектором напряженности
связан с вектором напряженности 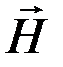 магнитного поля следующим соотношением:
магнитного поля следующим соотношением:
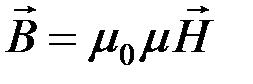 ,
,
где m 0 – магнитная постоянная, m – магнитная проницаемость среды.
|
|
|
Поскольку для вакуума m = 1, то с учетом приведенного соотношения может быть получена циркуляция вектора напряженности 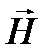 по произвольному замкнутому контуру L в следующем виде:
по произвольному замкнутому контуру L в следующем виде:
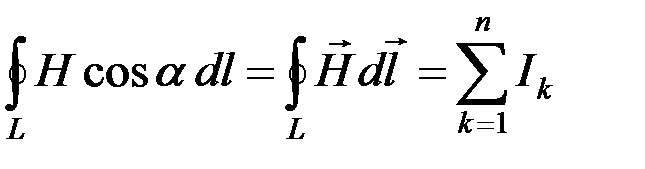 ,
,
то есть циркуляция вектора 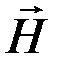 по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.
по произвольному замкнутому контуру L равна алгебраической сумме токов, охватываемых этим контуром L.
Сравнивая векторные характеристики электростатического (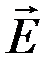 и
и 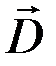 ) и магнитного (
) и магнитного ( и
и 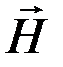 ) полей, следует отметить, что аналогом вектора напряженности
) полей, следует отметить, что аналогом вектора напряженности 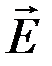 электростатического поля является вектор магнитной индукции
электростатического поля является вектор магнитной индукции  , так как векторы
, так как векторы 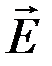 и
и  определяют силовые действия этих полей и зависят от свойств среды, а аналогом вектора электрического смещения
определяют силовые действия этих полей и зависят от свойств среды, а аналогом вектора электрического смещения 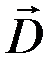 является вектор напряженности
является вектор напряженности 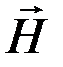 магнитного поля.
магнитного поля.
 2015-02-04
2015-02-04 602
602








