Квадратурный способ

Начальную задачу для ОДУ (1)-(2) можно заменить эквивалентным интегральным уравнением.

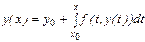(7)

При 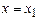из него получится равенство

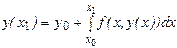(8)

Применение к интегралу в правой части равенства (8) простейшей одноточечной формулы прямоугольников дает приближенную формулу

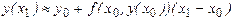
Правая часть которой, очевидно, совпадает с выражением (3) для подсчета значений 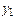. В общем случае расчетная формула (4) метода Эйлера получается численным интегрированием посредством простейшей формулы левых прямоугольников в равенстве

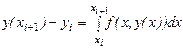(9)

В предположении, что на каждом i - том шаге в роли начальной точки 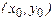выступает точка 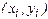. зная точность используемой квадратурной формулы легко прийти к тому же выражению локальной ошибки метода Эйлера, что и при других способах его построения.

Несколько простых модификаций метода Эйлера.

Очевидно, применение к интегральному равенству (7) других простейших квадратурных формул будет порождать новые методы численного интегрирования задачи Коши (1)-(2).

Применение к интегралу в (9) простейшей квадратурной формулы трапеций приводит к неявному методу

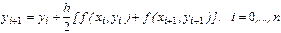(11)

который будем называть методом трапеций. Квадратурная формула трапеций, как известно, на порядок точнее формул правых и левых прямоугольников. Отсюда вытекает более высокий (на единицу) порядок точности метода трапеций (11) по сравнению с явным и неявным методами Эйлера(4) и (10), т.е. метод трапеций (15) – это метод второго порядка.

Некоторый интерес представляет собой совместное применение явного метода Эйлера и неявного метода трапеций.

По форме (11) представляет собой скалярную задачу о неподвижной точке относительно неизвестного 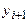. поэтому, если в правую часть (15) подставить хорошее начальное приближение 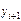, подсчитываемое по формуле (4), то тогда само это равенство можно считать шагом метода простых итераций для уточнения этого значения. Таким образом, получаем гибридный (двухшаговый) метод

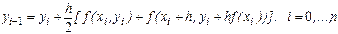(12)

который называют методом Хойна (методом Эйлера-Коши) или методом с пересчетом.

Построим другую пару формул с погрешностью на шаге такого же порядка. Интеграл в правой части заменим по формуле средних прямоугольников:

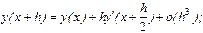или

;

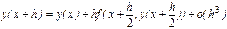Если положить 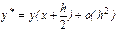, то .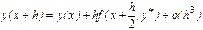

В качестве 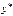- грубого приближения можно взять результат по формуле Эйлера с шагом :

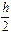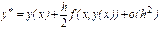
Этим соотношениям соответствуют расчетные формулы:

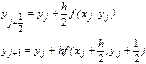(14)

этот метод будем называть методом Эйлера на полуцелой сетке.

Полученные методы относятся к семейству методов Рунге-Кутта.