Методы Рунге – Кутта

В процессе вычислений фиксированы некоторые числа:

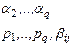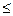0<j<i q;

Последовательно получаем:

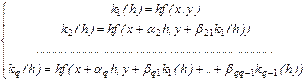
и полагаем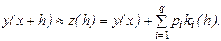

Рассмотрим вопрос о выборе параметров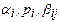

Обозначим 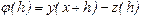- погрешность на шаге.

Если f(x,y)- гладкая функция своих аргументов, то 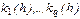тоже гладкие функции параметра h.

Пусть существуют производные 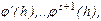а 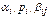выбраны так что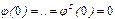

Кроме того, предположим, что существует 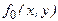, для которой .

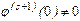Согласно формуле Тейлора выполняется равенство:

,

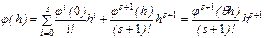где 0< 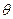<1 (15)

Величина 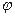(h) -называется погрешностью метода на шаге, а s - порядок погрешности метода.

1. При q=1 имеем:

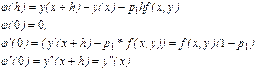
Равенство 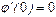выполняется для всех гладких функций f(x,y) только при .

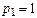Этому значению 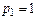соответствует метод Эйлера. Для погрешности этого метода на шаге, согласно (15) получаем выражение: .

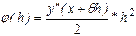Таким образом, s=1. Это метод первого порядка точности.

2. Рассмотрим q=2:

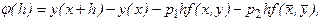где .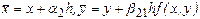

Вычисляем производные 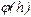, находим:

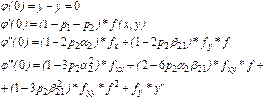
Соотношение 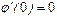, если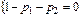

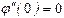, если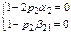

Таким образом, 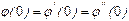при всех , если

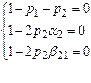
3 уравнения, 4 параметра. Задавая один из них произвольно, получим различные методы Рунге-Кутта с погрешностью второго порядка малости по h.

Например:

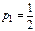
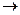
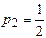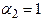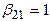, , , что соответствует формулам (12) - метод Эйлера пересчётом.

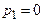
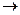
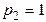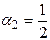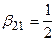, , , что соответствует формулам (14) - метод Эйлера с полуцелым шагом.

Так как 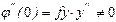, то нельзя построить формулы Рунге-Кутта с q=3, S=3;

3. Рассмотрим q=4, S=4.

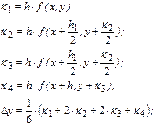(16)

Один из точных методов, S=4, 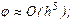он носит название метода Рунге – Кутта.

Численное решение дифференциальных уравнений высших порядков.

Рассмотрим однородное дифференциальное уравнение порядка (r)

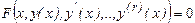
Задача Коши: требуется найти частное решение, удовлетворяющее (r) начальным условиям:

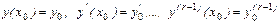
Одним из способов численного решения начальных задач для дифференциальных уравнений высших порядков является их сведение к соответствующим задачам для систем уравнений первого порядка.

Заменой переменных сводим задачу к системе (r) уравнений 1-го порядка.

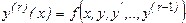
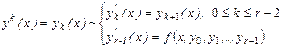
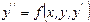
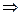
Например: 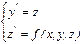начальные условия перепишутся в виде 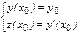т. д.

Методы Рунге-Кутта легко распространяются на системы дифференциальных уравнений 1-го порядка.

Например: рассмотрим систему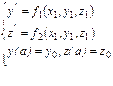

Приближённые решения 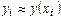и 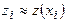этой системы в точках 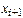последовательно вычисляется по формулам:

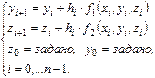метод Эйлера

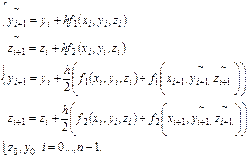
Метод Эйлера-Коши