Определение. Пусть 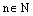 и
и 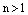 . Корнем n-й степени из комплексногочисла z называется комплексное число
. Корнем n-й степени из комплексногочисла z называется комплексное число 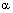 , такое, что
, такое, что 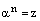 .
.
Теорема. (Формула корней из комплексного числа.)
Для любого ненулевого комплексного числа
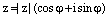 , где
, где 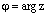 , существует ровно n корней n-й степенииз комплексного числа z и все они могут быть найдены по формуле
, существует ровно n корней n-й степенииз комплексного числа z и все они могут быть найдены по формуле
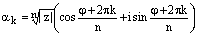 , (3)
, (3)
где 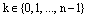 ,
, 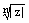 – арифметический корень n-й степени из положительного числа
– арифметический корень n-й степени из положительного числа 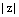 .
.
Доказательство. Обозначим
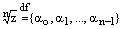 (4)
(4)
и докажем, что данное множество исчерпывает все множество корней n-й степени из комплексного числа z.
Доказательство проведем в 3 этапа. Сначала мы докажем, что всеэлементы множества (4) являются корнями n-й степени из комплексногочисла z. Затем мы покажем, что среди корней множества (4) нет равных. И, наконец, мы покажем, что любой корень n-й степени из комплексногочисла z является элементом множества (4).
1) По следствию 2 формулы Муавра 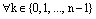
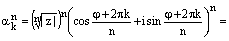
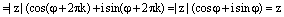 , ч.т.д.
, ч.т.д.
2) Допустим, что 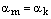 , где
, где 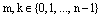 и
и 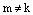 . Тогда по теореме о равенстве двух комплексных чисел в тригонометрическойформе записи следует, что равны их аргументы.
. Тогда по теореме о равенстве двух комплексных чисел в тригонометрическойформе записи следует, что равны их аргументы.
Но, аргумент числа 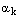 может отличаться от числа
может отличаться от числа 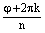 на числократное числу
на числократное числу 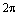 (т.е. на целое число оборотов) и аналогично для аргумента числа
(т.е. на целое число оборотов) и аналогично для аргумента числа 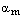 . Отсюда следует, что
. Отсюда следует, что 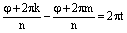 , где
, где 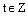 . Умножим это равенство на n:
. Умножим это равенство на n: 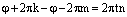 . Отсюда следует, что
. Отсюда следует, что 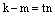 и т.к. по нашему предположению
и т.к. по нашему предположению 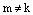 , то
, то 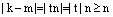 , чего не может быть, т.к.
, чего не может быть, т.к. 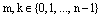 и
и 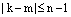 . Получили противоречие. Следовательно, среди корней вмножестве (10) нет равных, ч.т.д.
. Получили противоречие. Следовательно, среди корней вмножестве (10) нет равных, ч.т.д.
3) Пусть теперь комплексное число 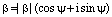 является корнем n-й степени из комплексного числа z, т.е.
является корнем n-й степени из комплексного числа z, т.е. 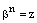 . Так как
. Так как 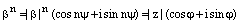 . Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства
. Отсюда, из тех же соображений, что и во второй части доказательства, следуют равенства 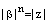 и
и 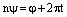 , где
, где 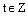 . Из первого равенства получаем, что
. Из первого равенства получаем, что 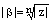 , а из второго следует
, а из второго следует 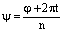 .
.
Далее, разделим целое число t на n с возможным остатком: 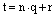 , где
, где 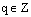 , а остаток r также является целым числом, но
, а остаток r также является целым числом, но 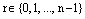 . Отсюда
. Отсюда
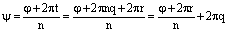 и
и
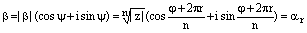 . Таким образом,корень
. Таким образом,корень 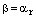 является корнем из множества корней (4), ч.т.д.
является корнем из множества корней (4), ч.т.д.
Теорема доказана.
Пример. Вычислить 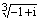 .
.
Решение. Запишем число 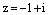 в тригонометрической форме записи:
в тригонометрической форме записи: 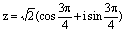 . Тогда
. Тогда
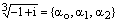 , где
, где
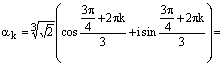
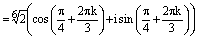 ,
, 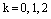 .
.
Ответ: 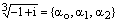 , где
, где
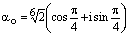 ,
,
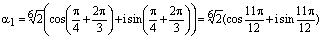 ,
,
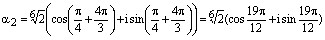
 2015-02-27
2015-02-27 778
778







