Алгебраическая форма комплексного числа

В алгебраической форме комплексное число записывают в виде 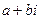, где а и b – вещественные числа. Два комплексных числа 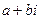и 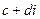равны тогда и только тогда, когда 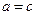, 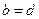. На основании этого определения решим несколько задач.

Задача 1.1. Найти .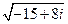

Решение. Предположим, что 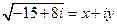.Тогда 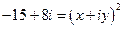или 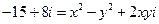. Используя условие равенства двух комплексных чисел, получаем систему уравнений для определения :

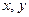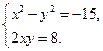
Решая систему, находим

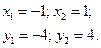
Откуда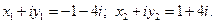

Итак, .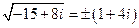

Задача 1.2. Найти 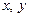так чтобы .

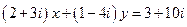Имеем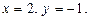

По определению произведением комплексных чисел 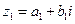и 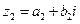называется число

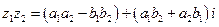Заметим, что комплексные числа можно перемножать как два многочлена первой степени с учетом того, что

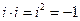Оперируя с комплексными числами, мы нередко получаем дроби вида 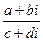, которые желательно упростить. Для этого надо умножить числитель и знаменатель дроби на число, комплексно сопряженное к знаменателю, то есть

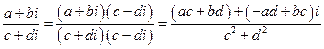28. Квадратні рівняння.

Квадратное уравнение — уравнение вида ax² + bx + c = 0, где a, b, c — некоторые числа (a ≠ 0), x — неизвестное.

Числа 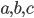называются коэффициентами квадратного уравнения.

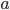§ называется первым коэффициентом;

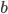§ называется вторым коэффициентом;

§ — свободным членом.

Приведенное квадратное уравнение — уравнение вида 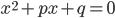, первый коэффициент которого равен единице ().

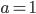Если в квадратном уравнении коэффициенты 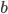и не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение 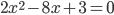. Если один из коэффициентов 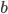или равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, .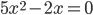

Значение неизвестного 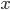, при котором квадратное уравнение обращается в верное числовое равенство, называется корнем этого уравнения. Например, значение 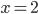является корнем квадратного уравнения 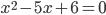, потому что 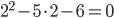или 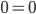— это верное числовое равенство.