С каждым комплексным числом 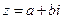 на плоскости связывается точка с координатами
на плоскости связывается точка с координатами 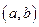 . Положение этой точки однозначно определяется расстоянием от начала координат
. Положение этой точки однозначно определяется расстоянием от начала координат 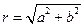 и углом
и углом 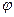 между положительным направлением вещественной оси и лучем, проведенным из начала координат в эту точку. Если угол отсчитывается в положительном направлении, то ему приписывается знак «+», а в противном случае знак «-». Комплексное число 0=0+0 i однозначно определяется расстоянием (равным 0) от начала координат, а потому ему значение угла не приписывается. Число
между положительным направлением вещественной оси и лучем, проведенным из начала координат в эту точку. Если угол отсчитывается в положительном направлении, то ему приписывается знак «+», а в противном случае знак «-». Комплексное число 0=0+0 i однозначно определяется расстоянием (равным 0) от начала координат, а потому ему значение угла не приписывается. Число 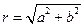 называется модулем комплексного числа
называется модулем комплексного числа 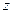 , а указанный выше угол
, а указанный выше угол 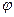 называется аргументом
называется аргументом 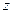 и обозначается
и обозначается 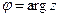 . Аргумент комплексного числа определяется с точностью до слагаемого, кратного
. Аргумент комплексного числа определяется с точностью до слагаемого, кратного 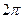 .
.
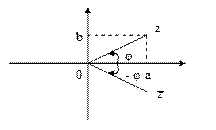
Из рисунка видно, что 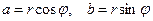 . Так что мы имеем следующий вид тригонометрической формы комплексного числа
. Так что мы имеем следующий вид тригонометрической формы комплексного числа
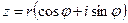 .
.
А число, комплексно сопряженное к z,имеет такую тригонометрическую форму 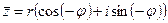 . Теперь, используя формулы для синуса и косинуса суммы (разности) двух углов, получаем
. Теперь, используя формулы для синуса и косинуса суммы (разности) двух углов, получаем
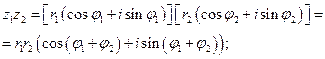
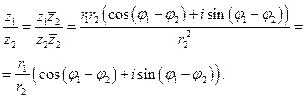
При возведении комплексного числа в степень с натуральным показателем можно воспользоваться следующей формулой, которая называется формулой Муавра.
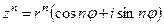 .
.
Для представления комплексного числа в тригонометрической форме очень полезно изобразить соответствующую этому числу точку (это избавит вас от ошибки в определении аргумента числа).
При решении задач часто используется следующий результат.
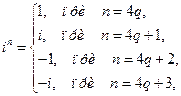
где 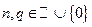 .
.
Приведем примеры решения некоторых задач.
30. Формула Муавра.
еорема. (Формула Муавра, 1707 г.)
Для любого целого числа n и любого действительного числа 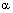 имеет место следующее равенство:
имеет место следующее равенство:
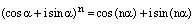 . (1)
. (1)
Доказательство. Разобьем доказательство на 3 этапа.
1) Пусть 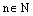 – натуральное число. Так как комплексное число
– натуральное число. Так как комплексное число 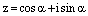 имеет модуль
имеет модуль 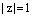 , то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
, то справедливость формулы Муавра в этом случае следует из следствия 2 теоремы об умножении комплексных чисел в тригонометрической форме записи.
2) Пусть теперь 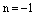 . Тогда
. Тогда
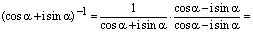
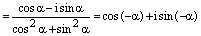 , ч.т.д.
, ч.т.д.
3) Пусть 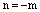 , где
, где 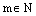 – натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и вполе комплексных чисел, имеем:
– натуральное число. Тогда по свойству целых степеней, которые справедливы в любом поле, в том числе и вполе комплексных чисел, имеем:
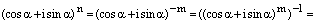
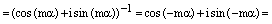
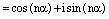 .
.
Здесь мы использовали уже доказанные случаи формулы Муавра возведения в натуральную степень и в степень, равную (–1).
Теорема доказана.
Следствие. (О целых степенях комплексного числа.)
Пусть 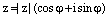 . Тогда
. Тогда 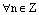
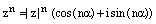 .
.
Доказательство предоставляется читателю.
 2015-02-27
2015-02-27 2222
2222
