2015-02-27
1372
Сначала рассмотрим способ разложения многочлена с целыми коэффициентами вида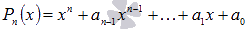 
, коэффициент при старшей степени равен единице.
В этом случае, если многочлен имеет целые корни, то они являются делителями свободного члена.
Пример.
Разложить на множители выражение 
.
Решение.
Проверим, имеются ли целые корни. Для этого выписываем делители числа -18: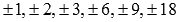 
. То есть, если многочлен имеет целые корни, то они находятся среди выписанных чисел. Последовательно проверим эти числа по схеме Горнера. Ее удобство еще и в том, что в итоге получим и коэффициенты разложения многочлена:
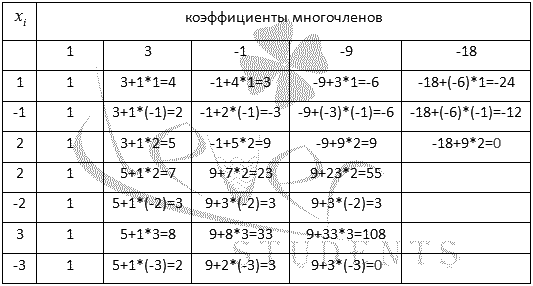
То есть, х=2 и х=-3 являются корнями исходного многочлена и он представим в виде произведения:
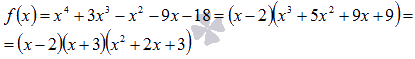
Осталось разложить квадратный трехчлен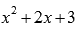 
.
Дискриминант этого трехчлена отрицательный, следовательно, он не имеет действительных корней.
Ответ:
.
Замечание:
вместо схемы Горнера можно было воспользоваться подбором корня и последующим делением многочлена на многочлен.
Теперь рассмотрим разложение многочлена с целыми коэффициентами вида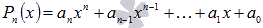 
, причем коэффициент при старшей степени не равен единице.
|
|
|
В этом случае многочлен может иметь дробно рациональные корни.
Пример.
Разложить на множители выражение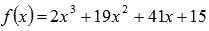 
.
Решение.
Выполнив замену переменной y=2x, перейдем к многочлену с коэффициентом равным единице при старшей степени. Для этого сначала домножим выражение на 4.
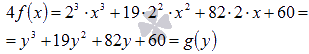
Если полученная функция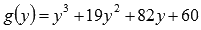 
имеет целые корни, то они находятся среди делителей свободного члена. Запишем их:
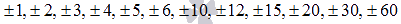
Вычислим последовательно значения функции g(y) в этих точках до получения нуля.
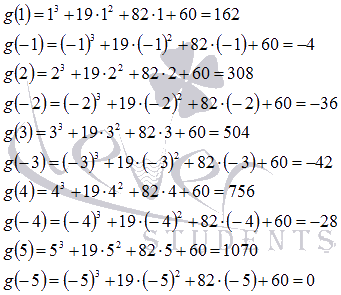
То есть, y=-5 является корнем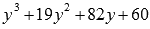 
, следовательно, 
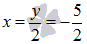является корнем исходной функции. Проведем деление столбиком (уголком) многочлена 
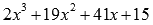на двучлен 
.
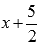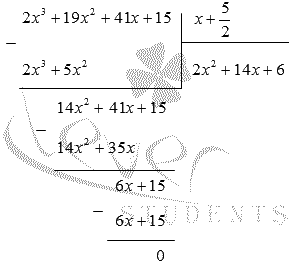
Таким образом,
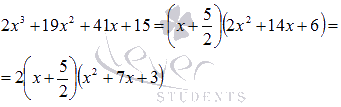
Проверку оставшихся делителей продолжать нецелесообразно, так как проще разложить на множители полученный квадратный трехчлен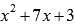 
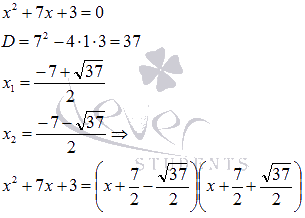
Следовательно,
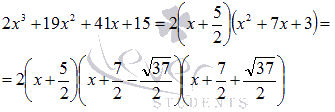
39. Незведені многочлени. Теорема про розклад многочлена у добуток незведених. Канонічний розклад многочлена.
