I. Любые два соседних многочлена не имеют общих корней
Теорема Штурма
Определение 2.7Последовательность многочленов 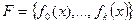 назовём последовательностью многочленов Штурма, если она удовлетворяет следующим условиям:
назовём последовательностью многочленов Штурма, если она удовлетворяет следующим условиям:
II. Если a – корень 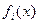 при i>0, то
при i>0, то 
IV. Если в окрестностях корня a многочлена 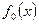 сам многочлен возрастает, то
сам многочлен возрастает, то 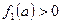 , а если убывает, то
, а если убывает, то 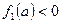
Для последовательности многочленов F и числа a определим w(a) – число перемен знака в числовой последовательности 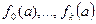 (нули игнорируем).
(нули игнорируем).
Теорема 2.21 Штурма
Число различных корней многочлена 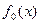 на отрезке
на отрезке 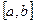 равно
равно 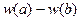 .
.
Доказательство. Пусть 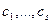 корни многочленов из ряда Штурма F, принадлежащие отрезку
корни многочленов из ряда Штурма F, принадлежащие отрезку 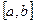 и упорядоченные в порядке возрастания. Поскольку, многочлен может изменить знак только при прохождении через корень, то для любых точек из интервала
и упорядоченные в порядке возрастания. Поскольку, многочлен может изменить знак только при прохождении через корень, то для любых точек из интервала 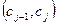 число перемен знака заведомо одно и тоже. Если
число перемен знака заведомо одно и тоже. Если 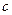 корень многочлена
корень многочлена 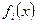 (i>0) то последовательность
(i>0) то последовательность 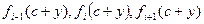 при достаточно малом по модулю значению y даёт только одну перемену знака, т.к. по условию II на концах стоят числа разных знаков. Следовательно, число перемен знака может измениться только при прохождении через корень многочлена
при достаточно малом по модулю значению y даёт только одну перемену знака, т.к. по условию II на концах стоят числа разных знаков. Следовательно, число перемен знака может измениться только при прохождении через корень многочлена 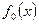 . По условию IV, число перемен знака может только уменьшаться.
. По условию IV, число перемен знака может только уменьшаться.
Пусть многочлен f(x) не имеет кратных корней. Построим последовательность многочленов: 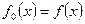 ,
, 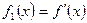 , и далее,
, и далее, 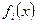 - остаток от деления
- остаток от деления 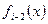 на
на 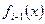 умноженный на -1.
умноженный на -1.
Данная последовательность многочленов будет последовательностью многочленов Штурма. Действительно, условие IV выполнено по свойству производной. Наибольший общий делитель многочлена и его производной равен 1, т.к. нет кратных корней. Таким образом, последний многочлен в ряду равен константе и не имеет вещественных корней. Из равенства 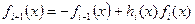 вытекает условие II. Подставив x=a, где a – корень
вытекает условие II. Подставив x=a, где a – корень 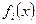 , получим
, получим 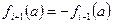 . Общего корня у соседних многочленов не может быть, так как его наличие приводит к существованию кратных корней у
. Общего корня у соседних многочленов не может быть, так как его наличие приводит к существованию кратных корней у 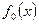 .
.
 2014-02-02
2014-02-02 1067
1067