Частные случаи

Известными примерами являются полином

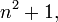
и так называемые простые числа-близнецы, для которых, однако, справедливость гипотезы не доказана.

Один из частных случаев гипотезы был доказан Дирихле. Так, для двух целых чисел, не имеющих общих делителей, арифметическая прогрессия вида

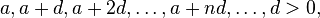
содержит бесконечное количество простых чисел.

40. Основна теорема алгебри. Многочлени над полем дійсних та комплексних чисел.

*4. Основная теорема алгебры

Не только уравнения вида ах² + bх + с = 0 или хⁿ - 1 = 0 разрешимы в поле комплексных чисел, но можно утверждать гораздо больше: всякое алгебраическое уравнение степени n с действительными или комплексными коэффициентами

f(х) = х_n + а_n-1х^n-1 + а_n-2х^n-2 +... + а₁х + a₀ = 0 (17)

разрешимо в поле комплексных чисел. Для случая уравнений 3-й и 4-й степеней эта теорема была установлена в XVI в. Тартальей, Кардано и другими: оказалось, что такие уравнения решаются посредством формул, подобных формуле квадратного уравнения, но значительно более сложных. В течение почти двух столетий длилось настойчивое изучение общего уравнения 5-й и более высоких степеней, но все усилия разрешить их теми же методами оказались напрасными. Когда молодому Гауссу в его докторской диссертации (1799) удалось впервые доказать, что решения существуют, то это уже было крупнейшим успехом; правда, вопрос о возможности обобщить на случай степеней ≥5 классические формулы, позволяющие находить корни с помощью рациональных операций и извлечения корней, оставался в то время открытым (см. стр. 146-147).

Теорема Гаусса утверждает, что, каково бы ни было алгебраическое уравнение вида (17), где n - целое положительное число, а коэффициенты а - действительные или даже комплексные числа, существует по крайней мере одно такое комплексное число α = с + di, что

f (α) = 0.

Число α называется корнем уравнения (17). Доказательство этой теоремы будет приведено в этой книге на стр. 299-301. Предположим пока, что теорема доказана, и выведем из нее другую теорему, известную под названием основной теоремы алгебры (было бы, впрочем, правильнее назвать ее основной теоремой комплексной числовой системы): всякий алгебраический полином степени n

f(x) = xⁿ + a_n-1x^n-1 +... + a₁x + a₀ (18)

может быть представлен в виде произведения ровно n множителей:

f(x) = (x - α₁)(x - α₂)...(x - α_n), (19)

где α₁, α₂,..., α_n - комплексные числа, корни уравнения f (х) = 0. Так, например, полином

f (x) = х⁴ - 1

разлагается на множители следующим образом:

f (х) = (х - 1)(x - i)(х + i)(х + 1).

Что числа α являются корнями уравнения f(х) = 0, это очевидно из самого разложения (19), так как при х = α_r один из множителей f (x), а следовательно, и сам полином f(x) обращаются в нуль.

В иных случаях не все множители x - α₁, х - α₂,... полинома f (х) степени n оказываются различными; так, в примере

f(x) = х² - 2х + 1 = (x - 1)(x - 1)

мы имеем только один корень х = 1, "считаемый дважды", или "кратности 2". Во всяком случае, полином степени n не может разлагаться в произведение более чем n различных множителей вида х - α, и соответствующее уравнение не может иметь более n корней.

При доказательстве основной теоремы алгебры мы воспользуемся - не в первый раз - алгебраическим тождеством

х^k - α^k = (х - α)(х^k-1 + αх^k-2 + α²х^k-3 +... + α^k-2х + α^k-1), (20)

которое при α = 1 служило нам для определения суммы геометрической прогрессии. Предполагая теорему Гаусса доказанной, допустим, что α = α₁ есть корень уравнения (17), так что

f (α₁) = αⁿ₁ + a_n-1α₁^n-1 + a_n-2α₁^n-2 +... + a₁α₁ + а₀ = 0.

Вычитая это выражение из f (х) и перегруппировывая члены, мы получим тождество

f(x) = f(x) - f(α₁) = (xⁿ - α₁ⁿ) + a_n-1(x^n-1 - α₁^n-1) +... + a₁(x - α₁). (21)

Пользуясь теперь формулой (20), мы можем выделить множитель х - α₁ из каждого члена и затем вынести его за скобку, причем степень многочлена, остающегося в скобках, станет уже на единицу меньше. Перегруппировывая снова члены, мы получим тождество:

f(х) = (х - α₁) g (х),

где g (х) - многочлен степени n-1:

g(x) = x^n-1 + b_n-2x^n-2 +... + b₁x + b₀.

(Вычисление коэффициентов, обозначенных через b, нас здесь не интересует.) Применим дальше то же рассуждение к многочлену g (x). По теореме Гаусса существует корень α₂ уравнения g (х) = 0, так что

g (х) = (x - α₂) h (x),

где h (х) - новый многочлен степени уже n-2. Повторяя это рассуждение n-1 раз (подразумевается, конечно, применение принципа математической индукции), мы, в конце концов, приходим к разложению

f (х) = (х - α₁)(х - α₂)(х - α₂)...(х - α_n). (22)

Из тождества (22) следует не только то, что комплексные числа α₁, α₂,..., α_n суть корни уравнения (17), но и то, что иных корней уравнение (17) не имеет. Действительно, если бы число у было корнем уравнения (17), то из (22) следовало бы

f (y) = (y - α₂)(y - α₂)...(y - α_n) = 0.

Но мы видели (стр. 122), что произведение комплексных чисел равно нулю в том и только в том случае, если один из множителей равен нулю. Итак, один из множителей y - α_r равен 0, т. е. y = α_r, что и требовалось установить.

41. Інтерполяційний многочлен Лагранжа.

Лагранжа интерполяционная формула

Так называется формула для нахождения интерполяционного многочлена L (x) степени m, принимающего в (m + 1)-й заданной точке xi промежутка [ a; b ] заданные значения f (xi), i = 0, 1, 2, …, m. Формула имеет вид: Легко видеть, что при подстановке в формулу значения х = х i все члены суммы, кроме i -го, обращаются в нуль (в числителе дробей, входящих в эти члены, появляются множители, равные нулю), а в i -м члене числитель становится равным знаменателю и дробь обращается в единицу, так что остается лишь множитель f (xi), т.е. получается, что L (xi) = f (xi). Таким образом, интерполяционный многочлен Лагранжа совпадает в заданных точках с заданными значениями неизвестной функции. Читать дальше... Важное значение имеет погрешность, которая имеет место при замене неизвестной функции у = f (x) интерполяционным многочленом. Для многочлена Лагранжа погрешность не превышает величины 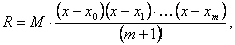где М – наибольшее значение модуля (абсолютной величины) (m +1)-й производной искомой функции на отрезке [ a; b ]. Из-за сложности вычислений коэффициентов по формуле Лагранжа неоднократно разными авторами, в том числе и в России, составлялись специальные таблицы коэффициентов. Рассматриваемая интерполяционная формула найдена французским математиком и механиком Ж. Л. Лагранжем в 1793 г..

42. Лінійні простори. Визначення, приклади. Лінійні підпростори.