В дальнейшем будем применять обозначение М|σ краткой записи высказывания: «автомат М в состоянии σ».
Определение 3.1. Говорят, что состояние σ i автомата М1 и состояние σ j автомата М2 эквивалентны, если М1| σ i и М2| σ j - под воздействием любой входной последовательности выдают одинаковые выходные последовательности. Если σ i и σ j не эквивалентны, то говорят, что они различимы. Обозначения М1 и М2 могут относиться к одному и тому же автомату.
Таким образом, σ i и σ j эквивалентны тогда и только тогда, когда, наблюдая внешние выходы, нельзя отличить автомат M1 находящийся в начальном состоянии σ i, от автомата М2, находящегося в начальной состоянии σ j [18]. Состояния σ i и σ j различимы тогда и только тогда, когда имеется хотя бы одна входная последовательность, подача которой как на М1| σ i так и на М2| σ j дает на выходах различные последовательности.
Эквивалентность σ i и σ j обозначается равенством σ i = σ j, а различимость σ i и σ j — неравенством σ i ≠σ j. Пользуясь определением 3.1, можно легко показать, что эквивалентные состояния обладают свойством рефлексивности (σ i = σ j), свойством симметричности (если σ i = σ j; то σ j = σ i) и свойством транзитивности (если σ i = σ j и σ j = σ k, то σ i = σ k). Следовательно, эквивалентность состояний может рассматриваться как обычное соотношение эквивалентности, которое применимо к множествам состояний любой мощности. Различимость состояний не обладает свойствами рефлексивности и транзитивности и, следовательно, может относиться только к парам состояний.
В некоторых случаях эквивалентность или различимость двух состояний одного и того же автомата могут быть установлены исследованием таблицы переходов данного автомата, Некоторые из этих случаев описываются с помощью следующих трех лемм.
Лемма 3.1. Пусть σ i и σ j —состояния автомата М. Если строки σ i и σ j в подтаблице z v автомата М различаются, то σ i ≠σ j.
Доказательство. Очевидно, существует по крайней мере один входной символ, при приложении которого к М|σ i и к M|σ j, на выходе М получаются различные выходные символы. Следовательно, по определению 3.1 σ i ≠ σ j.
Лемма 3.2. Пусть σ i и σ j — состояния автомата М. Если строки σ i и σ j в полной таблице переходов автомата М одинаковы, то σ i = σ j.
Доказательство. При приложении к М|σ i и к M|σ j любого входного символа выходные символы и следующие состояния в обоих случаях будут одинаковы. Поскольку М|σ i и M|σ j переходят в одно и то же состояние, их реакции на все подпоследовательности входных сигналов должны совпадать. Следовательно, по определению 3.1 σ i = σ j.
Лемма 3.3. Пусть σ i и σ j —состояния автомата М. Если строки σ i и σ j полной таблицы переходов автомата М становятся одинаковыми при замене каждого обозначения σ i и σ j (или наоборот), то σ i = σ j.
Доказательство. При приложении любого входного символа к М|σ i и к M|σ j выходные символы одинаковы в двух случаях: либо М|σ i и M|σ j переходят в одно и то же состояние, либо в состояния σ i и σ j (не обязательно соответственно). Если следующее состояние одно и то же, то реакции автомата на входные подпоследовательности будут совпадать. Если следующими состояниями являются σ i и σ j, то восстановится исходная ситуация, и приведенные выше соображения можно будет повторить, чтобы показать, что следующие выходные символы одинаковы в обоих случаях. Затем, по индукции, получим, что реакции при σ i и σ j на любую входную последовательность будут одинаковыми, откуда следует, что σ i = σ j
Пары строк, обладающие свойством, приведенным в лемме 3.1, называются явно различимыми, а состояния, стоящие в основном столбце в этих строках, — явно различимыми состояниями. Пары строк, обладающие свойствами,
указанными в леммах 3.2 и 3.3, называются явно эквивалентными, а состояния, стоящие в основном столбце в этих строках,—явно эквивалентными состояниями.
Таким образом, имеем:
Теорема 3.1. Если состояния σ i и σ j явно различимы, то σ i ≠σ j, а если состояния σ i и σ j, явно эквивалентны, то σ i и σ j.
Следует отметить, что утверждение, обратное теореме 3.1, несправедливо, т. е. не каждая пара различимых состояний является явно различимой и не каждая пара эквивалентных состояний явно эквивалентной. Используя определения, введенные в § 2.3, можно заключить, что в явно минимальном
автомате все пары состояний различимы, а в явно сократимом автомате имеется по крайней мере одна пара эквивалентных состояний.
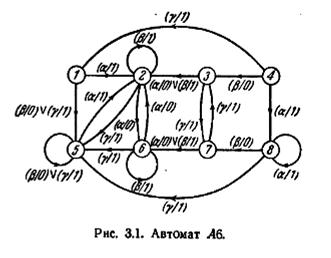
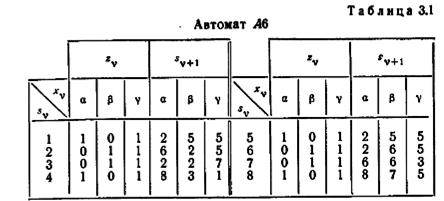
Для иллюстрации лемм 3.1—3.3 рассмотрим автомат A6, представленный графом переходов, изображенным на рис. 3.1, и таблицей переходов 3.1. Из таблицы переходов видно, что строки 1 и 5 одинаковы, а строки 2 и 6 становятся одинаковыми, если каждую цифру 2 заменить на цифру 6 (или каждую цифру 6 заменить на цифру 2). Следовательно, состояния в парах {1,5} и {2, 6} являются эквивалентными. Рассмотрение подтаб-
лицы zv показывает также, что ни одно состояние из множества {1, 4, 5, 8} не может быть эквивалентным какому-либо состоянию из множества {2, 3, 6, 7}.
 2015-02-27
2015-02-27 878
878








