Простые безусловные диагностические эксперименты

Результаты, полученные в предыдущем параграфе, наводят на мысль о методе решения диагностической задачи для m состояний с помощью кратчайшего простого безусловного эксперимента во всех случаях, когда решение с помощью такого эксперимента существует.

Алгоритм 4.2. Даны автомат М и его множество допустимых начальных состояний

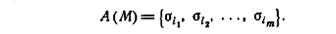
Требуется найти начальное состояние М с помощью кратчайшего простого безусловного эксперимента. (1) Построим диагностическое дерево для М и А (М). (2) Найдем любую диагностическую последовательность ε (А), описываемую этим деревом. Если ни одна такая последовательность деревом не описывается, то не существует решения с помощью простого безусловного эксперимента. (3) Перечислим реакции М|σi₁, М|σi₂,..., М|σi_m на ε(A).(4) Подадим ε(А) на M и зафиксируем реакцию. Начальным состоянием автомата является состояние σi _k, для которого реакция, упомянутая в (3), совпадает с зафиксированной реакцией.

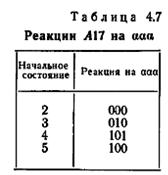
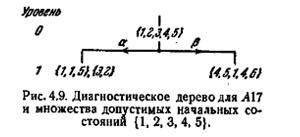
Алгоритм 4.2 может быть продемонстрирован на примере автомата A17, показанного на рис. 4.3, и множества допустимых начальных состояний {2, 3, 4, 5}. В этом случае диагностическое дерево, представленное на рис. 4.7, показывает, что минимальной диагностической последовательностью является последовательность aaa. В таблице 4.7 перечислены реакции состояний 2, 3, 4 и 5 на aaa. Эти реакции, как можно было ожидать, являются различными и могут служить в качестве критерия для распознавания начального состояния A17, когда оно принадлежит заданному множеству допустимых начальных состояний. Другой пример приведен на рис. 4.8, выявляющем, что минимальными диагностическими последовательностями для A17 и множества допустимых начальных состояний {1, 2} являются последовательности β aaa и β a β a. Для m = 2 диагностическая задача сводится к диагностической задаче для двух состояний, для которой по теореме 4,1 всегда существует решение с помощью простого безусловного эксперимента. В этом случае минимальная диагностическая последовательность может быть более удобно определена через таблицы P_k, как описано в § 4.4. Для m > 2 решение посредством простого безусловного эксперимента существует не всегда, как показано с помощью диагностического дерева для A17 и множества допустимых начальных состояний {1, 2, 3, 4, 5}, изображенных на рис. 4.9.

Используя лемму 4.4, мы теперь можем подвести следующие итоги.

Теорема 4.3. Если диагностическая задача для автомата с n состояниями и m допустимыми состояниями вообще может быть решена путем проведения простого безусловного эксперимента, то она может быть решена путем простого безусловного эксперимента длины l, где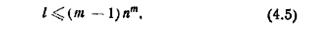

Решение диагностической задачи для т состояний непосредственно может быть применено к следующей задаче: известно, что данный автомат М является автоматом М₁ в состоянии, принадлежащем множеству А(М), или автоматом М₂ в состоянии, принадлежащем множеству А(М₂),..., или автоматом M _N в состоянии, принадлежащем множеству A(M _N). Требуется распознать автомат М и его начальное состояние. В предположении, что М₁, М_2,..., M _N являются сравнимыми и для них имеются таблицы переходов, вышеупомянутая задача в точности представляет собой диагностическую задачу для т состояний для расщепляемого автомата ∆(М₁, М_2,..., M _N) и множества допустимых начальных состояний А(М₁)UА(М₂)U... UA (M _N). Основное предположение о том, что данный автомат М является минимальным, в данном случае означает, что каждый автомат М: минимален и что ни одно состояние в автомате М₁ не является эквивалентным ни одному состоянию в автомате M_j (j ≠ i).