Регулярные условные установочные эксперименты

Регулярные безусловные установочные эксперименты, описанные в § 4.15, могут быть преобразованы в регулярные условные установочные эксперименты путем применения подпоследовательностей по одной и выбора следующей подпоследовательности на основе реакции на предыдущую подпоследовательность. Подход такой же, как в случае безусловного эксперимента, за исключением того, что на основании наблюдаемой реакции все, кроме одного, σ-множества из G_k (k≥1) могут быть устранены из дальнейших рассмотрений.

Алгоритм 4.8. Даны автомат М и его множество допустимых начальных состояний А(М); требуется определить конечное состояние М с помощью простого условного эксперимента. (1) Пусть А(М) есть g₀. Полагаем k = 0. (2) (а) Если g_k неоднородно, то определяем регулярную подпоследовательность, скажем ε_k, для g_k. Прилагаем ε_h к M и полагаем, что g'_k является подмножеством g_k. которому может быть свойственна наблюдаемая реакция. Пусть g_k+1есть ε_k-преемник g'_k. Увеличиваем k на 1 и возвращаемся к (2). (б) Если g_k однородно, то конечное состояние М есть состояние, содержащееся в g_k. Если g_k в алгоритме 4.8 не является однородным, то мощность g_k+l должна быть меньше, чем мощность g_k. Следовательно, если мощность А(М) есть m, то число подпоследовательностей не превышает m — 1. Для g_k мощности r всегда имеется регулярная подпоследовательность ε_K, длина которой не превышает n—r+1, где n есть общее число состояний в М. Следовательно, общая длина установочного эксперимента не может превосходить

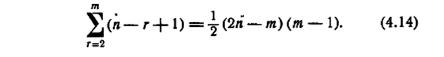
Таким образом, мы имеем следующую теорему.

Теорема 4.13. Установочная задача для автомата с n состояниями и т допустимыми состояниями может быть всегда решена с помощью простого условного эксперимента длины l и порядка d, где

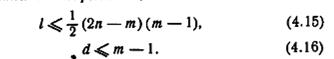
Можно отметить, что регулярный условный установочный эксперимент, построенный с помощью алгоритма 4.8, никогда не бывает длиннее, чем регулярный безусловный установочный эксперимент, построенный по алгоритму 4.7.

Таблица 4.14 демонстрирует регулярный условный эксперимент для A17, показанного на рис. 4.3, и множества допустимых начальных состояний {1, 2, 3, 4, 5}, когда истинное начальное состояние есть 4. Первый столбец содержит для справки перечень состояний, через которые A17 проходит по мере проведения эксперимента (эти состояния, конечно, не известны экспериментатору). В этом примере g₀ есть {1, 2, 3, 4, 5}, a ε₀ есть а. Когда а подается на A17, наблюдаемая реакция есть 1, из которой может быть выведено, что g´₀ есть {4, 5}. Тогда g₁ есть а -преемник g'₀ a именно {3, 2}. Подача ε1 = aa на A17 дает реакцию 01, из которой может быть выведено, что g´₁ есть {3}. Тогда g₂ есть aa -преемник g´₁, а именно {2}. Так как g₂ однородно, можно сделать заключение, что конечное состояние A17 есть 2.

Рис. 4.17 показывает автомат, обозначенный М*, в котором могут быть достигнуты границы теоремы 4.13[27]. Как показано на рисунке, множеством.состояний М* является {1, 2,..., n}, входной алфавит есть {ξ ₁ξ _2... ξ_n-1}, а выходной алфавит—{0, 1}. Выходной символ 1 генерируется только тогда, когда ξ_n-1 подается в состоянии n. Из структуры М* можно увидеть, что если этот автомат, находясь в состоянии 1, 2,...,i, j (j > i), подвергается воздействию любого входного символа, отличного от ξ_j-1, то состояниями-преемниками, соответственно, являются 1,2,...,i, j или 1,2,..., i, j— 1. По отношению к установочному дереву для М* и множеству допустимых начальных состояний {1, 2,..., m) под этим понимается, что кратчайший путь, ведущий из {1, 2,..., m) к A-группе, содержащей, по крайней мере, два а -множества, есть путь, описывающийся входной последовательностью ξ_m-1ξ _m... ξ_n-1; A-группа, к которой ведет этот путь, есть {1, 2,...., m — 1}, {n}. Тогда по индукции кратчайший путь, ведущий от {1, 2,...., m) к однородной A-группе, есть путь, описывающийся входной последовательностью ξ_m-1ξ _m... ξ_n-1 (Длины n — m + 1), за которой следует ξ_m-2ξ _m-1... ξ_n-1 (длины n—m+2) за которой ξ₁ξ_2... ξ_n-1 (длины n—1). Длина этой последователь

ности есть (2n— m)(m — 1)/2, т. е. совпадает с выражением (4.14). Путь ведет к A-группе {1}, {n}, {п},..., {n}, которая содержит m простых (и, следовательно, однородных)

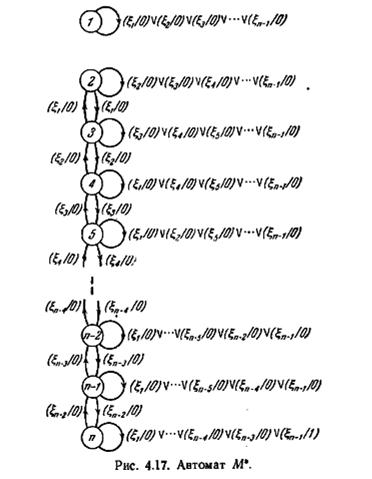
σ-множеств. Рис. 4.18 показывает установочное дерево для автомата М* и множества допустимых начальных состояний {1, 2,..., m}; на этом рисунке все оконечные ветви опущены, и единственный показанный путь есть путь, описывающий минимальную установочную последовательность, упомянутую выше. Ясно, что если начальным состоянием М* оказалось состояние 1, то кратчайший условный установочный

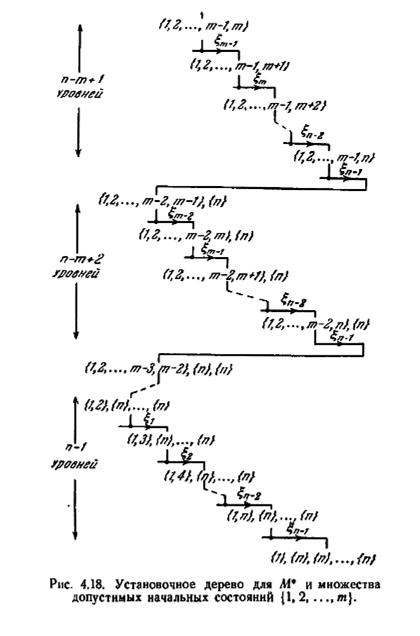
эксперимент для М* и множества допустимых начальных состояний {1, 2,..., m} должен состоять из m — 1 подпоследовательностей, совокупная длина которых задана верхней границей выражения (4.15). Автомат М* показывает также, что кратчайший безусловный установочный эксперимент может иметь длину (2n—m)(m — 1)/2 символов.

Заметим, что так как конечная A-группа на рис. 4.18 является простой A-группой, показанный путь описывает минимальную диагностическую последовательность (так же как минимальную установочную последовательность). Поэтому автомат М* показывает, что простой безусловный или условный диагностический эксперимент может иметь длину, равную верхней границе l (4.15).