Множество элементов с определенной на нем групповой операцией называется группой, если выполняется следующие условия:
1. Замкнутость gi 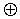 g j= gk
g j= gk 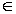 G в результате операции с двумя элементами группы получается третий, так же принадлежащий этой группе.
G в результате операции с двумя элементами группы получается третий, так же принадлежащий этой группе.
2. Ассоциативность (сочетательность) (gi 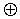 gj)
gj) 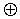 gk = gi
gk = gi 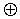 (gj
(gj 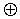 gk)
gk)
3. Наличие нейтрального элемента gj 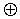 e = gj
e = gj
4. Наличие обратного элемента. gi 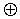 (gi)-1= e
(gi)-1= e
Если выполняется условие gi 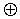 gj = gj
gj = gj 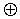 gi, то группа называется коммутативной.
gi, то группа называется коммутативной.
Множество кодовых комбинаций n-элементного кода является замкнутой группой с заданной групповой операцией сложение по модулю 2.
Поэтому используя свойство замкнутости относительно операции 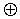 2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.
2, множество всех элементов можно задать не перечислением всех элементов, а производящей матрицей.
Все остальные элементы, кроме 0, могут быть получены путем сложения по модулю 2 строк производящей матрицы в различных сочетаниях.
В общем случае строки производящей матрицы могут быть любыми линейно независимыми, но проще и удобнее брать в качестве производящей матрицы – единичную.
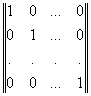
 2015-02-04
2015-02-04 380
380








