2015-02-27
698
Рассматривается уравнение материального баланса, используемое в дифференциальной форме для элементарного реакционного объёма dV. Составление УМБ для элемента dV, (л 2, стр. 83.)
Требования dV:
Все технологические параметры: (Т, Р, С, U…) выровнены по dV, равны между собой и остаются постоянны за время dτ (лекция 2, стр. 129).
Уравнение материального баланса для dV:
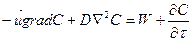(15.1)
где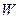 
– массовая скорость кристаллизации загрязняющего вещества. (см. реакцию 14.1).
Вблизи поверхности твёрдые частицы в пределах гидродинамического пограничного слоя δ (рис. 3.2), продольная скорость жидкости U убывает до 0, причём поперечный конвективный перенос отсутствует.
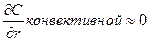
и массоперенос к поверхности твёрдой частицы определяется главным образам диффузией (в сферических координатах).
Уравнение диффузии записывается в следующем виде:
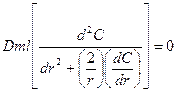(15.2)
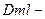коэффициент молекулярной диффузии (
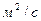), табличная величина.
граничные условия (рис.3.2)
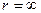
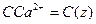
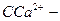коэффициент загрязнения вещества,
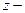продольная координата (рис. 14.2 б)
Решение дифференциального уравнения 15.2 позволяет получить распределение концентрации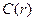 
вблизи твёрдой частицы.
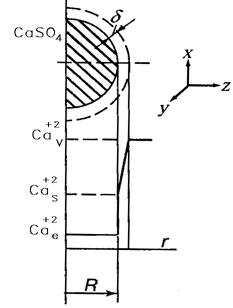
и решений уравнения (15.2)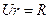 
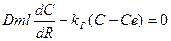(15.4)
На поверхности твёрдой частицы: протекает реакция.
(14.1) с образованием нерастворимого соединения содержащего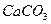 
, который откладывается в виде отложения на поверхности шарообразной частицы. За счет этих процессов частицы увеличиваются в размере.
С учётом (15.2 и 15.4)
Решение в виде
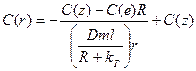(15.5)
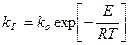– уравнение Аррениуса
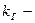константа скорости реакции.
Для уравнения (14.1) реакция I порядка
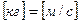
и массовая скорость кристаллизации
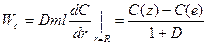кг (15.7)
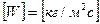
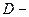критерий Дамкелера. Он характеризует интенсивность, относительность кинетических и внешне диффузионных процессов.
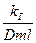(процессы массопереноса этим распределением).
Уравнение 15.6 и 15.5 – представляет собой математическую модель, составленную для одиночной шарообразной частицы (рис. 14.2 а3), см. затравочные кристаллы.
