Равномерного распределения равномерного распределения

Распределение вероятностей называется равномерным, если плотность распределения всюду равна нулю, кроме интервала (а, Ь), где она постоянна.

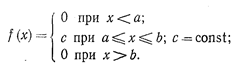
Математическое ожидание случайной величины Х, равномерно распределено на участке от а до Ь:

Далее дисперсия определяется следующим образом:

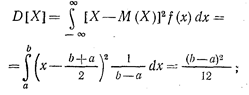
А среднее квадратическое отклонение - по следующей зависимости:

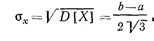
Вероятность попадания равномерно распределенной случайной величины на участок (α, β), представляющий собой часть интервала [а, b], определяется зависимостью:

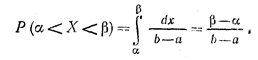
Графически, вероятность попадания очередного значения случайной величины в интересующий нас заданный интервал равна заштрихованной площади графика дифференциальной функции плотности распределения вероятностей (рис. 15.4.3).

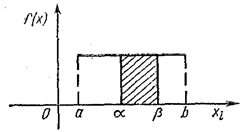
Рис. 15.4.3. График наблюдённой функции