Классификация основных видов статистических графиков

Для графического представления статистических данных используются самые раз­нообразные виды графиков (рис. 4.2 и 4.3). Их можно классифицировать по разным при­знакам: характеру графического образа, способу построения и назначению (содержанию).

По характеру графического образа различают графики объемные, линейные и пло­скостные (рис. 4.2).

способу построения графики можно разделить на диаграммы и статистические карты (рис. 4.3).

Диаграмма представляет собой чертеж, показывающий соотношение статистиче­ских данных при помощи разнообразных геометрических и изобразительных средств.

Статистические карты предназначены для графического изображения одноимен­ных показателей, относящихся к разным территориям. Для этого в основу изображения берется географическая карта. Изображение на карте статистических данных называется картограммой или картодиаграммой.

По содержанию или назначению можно выделить графики сравнения в простран­стве, графики относительных величин (структуры, динамики и т.п.), графики вариационных рядов, графики взаимосвязанных показателей и графики размещения по территории (рис. 4.3).

Диаграммы сравнения
Различные виды диаграмм применяются для сравнения одноименных статистиче­ских данных, характеризующих разные территории или объекты. Наиболее распростра­нённым видом таких диаграмм являются столбиковые диаграммы. Они представляют собой график, в котором различные величины представлены расположенными в высоту прямоугольниками («столбиками») одинаковой или разной высоты. Столбиковые диаграммы применяются для сравнения некоторых объектов во времени.

Построение такого рода диаграмм требует только одной вертикальной масштаб-вой шкалы, которая определяет высоту каждого столбика.

Масштабная шкала должна начинаться с нуля, быть непрерывной и на ней записываются лишь круглые или округленные значения.

Столбики должны быть даны на некотором, одинаковом для всех расстоянии или вплотную друг к другу. Ширина столбиков берется произвольной. На шкале должна быть указана единица измерения. При выборе масштаба надо рассчитать так, чтобы максимальное число было представлено на графике.

Пример. Требуется изобразить с помощью столбиковой диаграммы данные о тру­доустройстве граждан органами государственной службы занятости региона (цифры условные): в 2004 г. трудоустроено 2822 чел,; в 2003 г. - 2398 чел.; в 2002 г. - 2406 чел.; в

2001 г. - 2218 чел. Примем масштаб: 500 чел. соответствует 1 см. Тогда высота первого столбика (трудоустройство в 2001 г.) будет равна 4,4 см (1 см*2218/500), высота второго ' (в 2002 г.)-4,8 см; высота третьего (в 2003 г.)-4,79 см; высота четвертого (в 2004 г.)-5,6 см.

Наглядность данной диаграммы достигается сравнением высоты столбиков (рис. 4.4).

На рис. 4.5 с помощью столбиковой диаграммы показана структура посевных пло­щадей сельхозпредприятий N-ой области РФ за 2004 г. (цифры условные). На этой диаграмме столбики располагаются вплотную по группам объектов в пространстве/

Масштаб принят такой, что каждым 5000 тыс. га соответствует отрезок в 1 см.

Если прямоугольники, изображающие показатели, расположить не по вертикали, а

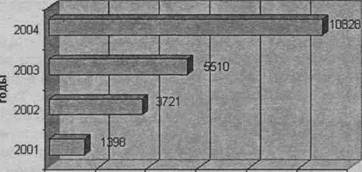
по горизонтали, то диаграмма получит название ленточной. В качестве примера приведем полосовую диаграмму сравнения, характеризующую данные о реализации минеральных удобрений сельхозпредприятиями в N-ом регионе за 2001-2004 гг. (рис. 4.6).

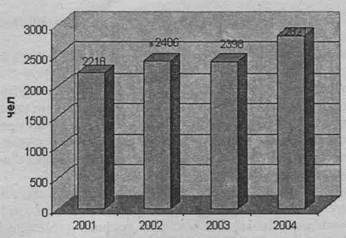
Рис. 4.4. Динамика трудоустройства граждан органами государственной службы занятости в регионе за 2001-2004 гг.

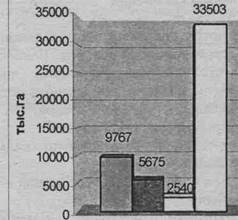
Рис. 4.5. Структура посевных площадей сельхозпредприятий N-ой области РФ в 2004г.

0 2000 4000 6000 8000 10000 12000

Тыс.т

Рис. 4.6. Динамика реализации минеральных удобрений сельскохозяйственными предприятиями в N-ом регионе за 2001-2004 гг.

Иногда разница между наименьшими и наибольшими значениями сравниваемых данных настолько велика, что установление подходящего масштаба для столбиков или полос оказывается затруднительным. В этих случаях вместо столбиковой (полосовой) диаграммы целесообразно применить плоскостную (двухмерную) диаграмму - квадрат­ную или круговую. Принцип построения этих диаграмм заключается в том, что величины сравниваемых данных изображаются площадями квадратов или кругов. Иными словами, площади квадратов (кругов) должны быть пропорциональны величинам изображаемых явлений, но сами площади квадратов (кругов) пропорциональны квадратам их сторон (ра­диусов). Следовательно, стороны квадратов или радиусов кругов должны быть пропорциональны корням квадратным из величин изображаемых статистических данных.

Пример. Необходимо с помощью квадратной диаграммы изобразить реализацию

молочных продуктов предприятиями розничной торговли в одном из регионов за 2004 г.

по следующим данным:

Товар	Товарооборот, млн. руб.
творог	11
сметана	16
молоко	19

Для построения квадратной диаграммы сначала извлечем квадратные корни из чи­сел: √11=3,32; √16=4; √19=4,36. Затем установим масштаб, например, примем 1см-1,5 млн. руб. Тогда сторона 1-го квадрата составит 2,2см (3,32:1,5); 2-го - 2,7см; 3-го - 2,9см (4,36:1,5). Далее строим квадраты.

Для правильного построения диаграммы квадраты необходимо расположить на одинаковом расстоянии друг от друга, а в каждой фигурке указать числовое значение, которое она изображает, не приводя масштаба измерения (рис. 4.7).
19

16

11

творог сметана молоко
Рис. 4.7. Реализация молочных продуктов предприятиями розничной торговли в одном из регионов в 2004 г., млн. руб.

Круговая диаграмма строится аналогично квадратной с той разницей, что находим, величину радиуса для каждого круга.

Пример. По данным об иностранных инвестициях в экономику РФ по основным^: странам-инвесторам за 2002 г. построить круговые диаграммы:

Страна	Германия	Кипр	Швейцария
Инвестиции, млн долларов США (х)	4001	2327	1349
√x	63,25	48,24	36,7
R	3,2	2,4	1,8

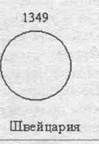
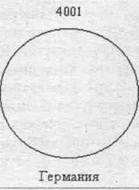
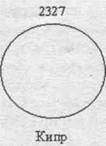
Примем 1 см - 20 млн. долл., тогда радиус 1-го круга будет 3,2 см (63,25:20), • 2-го круга - 2,4 см; 3-го круга -1,8 см. (рис. 4.8).

Рис. 4.8. Иностранные инвестиции в экономику РФ по основным странам-инвесторам за 2002 г., млн. долларов США

Диаграммы, предназначенные для популяризации, иногда строятся в виде стандартных фигур-рисунков, характерных для изображаемых статистических данных, что } лает диаграмму более выразительной, привлекает к ней внимание. Такие диаграммы называются фигурными или изобразительными. Каждая фигурка имеет одинаковый размер и принимается за определённую величину изображаемых статистических данных.

Пример. Изобразим в виде фигурной диаграммы количество проданных магнитофонов в N-ом регионе за 2001-2004 гг. по следующим данным:

Годы	2001	2002	2003	2004
Продано, тыс. шт.	1977	862	875	995

П

Рис. 4.9.Динамика продажи магнитофонов за 2001 - 2004.

римем условно за один знак 300 тыс. штук магнитофонов. Тогда продажа магнитофонов в 2001 г. в размере 1977 тыс. штук будет изображена в количестве 6,6 магнитофона, в 2002 г. - 2,9 магнитофона, в 2003 г. - 2,9 магнитофона, в 2004 г. - 3,3 магнитофона (рис. 4.9).

Недостаток фигурных диаграмм заключается в том, что во многих случаях прихо­дится либо округлять изображаемые данные, либо изображать, кроме целых фигур, их части, размер которых на глаз оценивать трудно.

Для графического изображения трех взаимосвязанных показателей, один из кото­рых равен произведению двух других, российский статистик проф. В.Е.Варзар предложил использовать прямоугольную диаграмму, названную им «статистическим знаком». В на­стоящее время такие диаграммы часто называют знаком Варзара.

Знак Варзара строится в виде прямоугольника, основание которого пропорцио­нально одному показателю-сомножителю, а высота - второму показателю сомножителю. Тогда произведение этих показателей, т.е. третий показатель, будет изображаться площа­дью прямоугольника.

Пример. Имеются следующие данные в 2001 г. по всему миру:

ВНП - 46403 млрд. долл.

ВНП на душу населения - 7570 долл.

Средняя численность населения - 6,1298 млрд. чел.

Нужно изобразить эти данные с помощью знака Варзара (рис. 4.10). Взаимосвязь этих по­казателей можно представить в виде

Рис. 4.10. Зависимость общего производства ВНП от производства ВНП на душу

населения и средней численности населения мира в 2001 г.

Диаграммы структуры
Вторую большую группу показательных графиков составляют структурные диаграммы. Это такие диаграммы, в которых отдельные статистические совокупности сопоставляются по их структуре, характеризующейся соотношением разных параметров совокупности или ее отдельных частей.

Широко распространенный метод графического изображения структуры статисти­ческих данных заключается в составлении структурных круговых или секторных диа­грамм. Секторные диаграммы удобно строить следующим образом: вся величина явле­ния принимается за сто процентов, рассчитываются доли отдельных частей в процентах. Крут разбивается на секторы пропорционально частям изображаемого целого. Таким об­разом, на 1% приходится 3,6 градуса. Для получения центральных углов секторов, изо­бражающих доли частей целого, необходимо их процентное выражение умножить на 3,6 градуса. Секторные диаграммы позволяют не только разделить целое на части, но и сгруппировать отдельные части, давая как бы комбинированную группировку долей по двум признакам.

Пример. Рассмотрим построение секторной диаграммы по следующим данным о структуре иностранных инвестиций в РФ в 2002 году:

Тип инвестиций	прямые	портфельные	прочие
Доля инвестиций, в %	20	2	78

Построение секторной диаграммы начинается с определения центральных углов секторов. Для этого процентное выражение отдельных частей совокупности умножим на 3,6 градуса, т.е. 20*3,6=72°; 2*3,6=7,2°; 78*3,6-280,8°. По найденным значениям углов круг делится на соответствующие сектора (рис. 4.11).

Рис. 4.11. Удельный вес иностранных инвестиций в РФ за 2002 г.
Другим видом структурных статистических диаграмм являются диаграммы удель­ных весов, отражающие структуры сравниваемых совокупностей по процентному соот­ношению в них отдельных частей, выделяемых по тому или иному количественному или атрибутивному признаку. Эти диаграммы получены путем преобразования простой поло­совой диаграммы с подразделенными полосами. Полосовые диаграммы удельных весов могут вскрыть экономически существенные особенности многих изучаемых экономиче­ских явлений.

Пример. Необходимо изобразить графически следующие данные, характеризую­щие структуру потребительских расходов населения в N-ом регионе за 2003-2004 гг. (в процентах):

Изобразим эти данные графически в виде полосовой диаграммы, цель которой- показать изменение удельных весов потребительских расходов населения за два года(рис.4.12).

Рис. 4.12. Динамика удельного веса потребительских расходов населения

в N-ом регионе за 2003-2004 гг.
Значительными преимуществами полосовых структурных диаграмм по сравнению с другими видами является их большая емкость, возможность отразить на небольшом пространстве большой объем полезной информации.

Секторные диаграммы выглядят убедительно при существенных различиях срав­ниваемых структур, а при небольших различиях они могут быть недостаточно вырази­тельны.

Диаграммы динамики
Для изображения и внесения суждений о развитии явления во времени строятся диаграммы динамики. В рядах динамики используются для наглядного изображения явле­ний многие диаграммы: столбиковые, ленточные, квадратные, круговые, линейные, ради­альные и другие. Выбор вида диаграмм зависит в основном от особенностей исходных данных, от цели исследования. Например, если имеется ряд динамики с неравноотстоя-щими уровнями во времени (1913, 1940, 1950, 1980,2000, 2005 гг), то часто для наглядно­сти используют столбиковые, квадратные или круговые диаграммы. Они зрительно впе­чатляют, хорошо запоминаются, но не годны для изображения большого числа уровней, так как громоздки, и если число уровней в ряду динамики велико, то целесообразно при­менять линейные диаграммы, которые воспроизводят непрерывность процесса развития в виде непрерывной ломаной линии.

Для построения линейных диаграмм используют систему прямоугольных коорди­нат. Обычно по оси абсцисс откладывается время (годы, месяцы и т.д.), а по оси ординат наносят масштабы для отображения явлений или процессов. Особое внимание следует об­ратить на масштаб осей координат, так как от этого зависит общий вид графика. Обеспе­чение равновесия, пропорциональности между осями координат необходимо в диаграмме, так как нарушение равновесия дает неправильное изображение развития явления. Если масштаб для шкалы на оси абсцисс очень растянут по сравнению с масштабом на оси ор­динат, то колебания в динамике явлений мало выделяются, и наоборот, преувеличение масштаба по оси ординат по сравнению с масштабом на оси абсцисс дает резкие колеба­ния. Если в ряду динамики данные за некоторые годы отсутствуют, это должно быть учтено при построении графика. Равным периодам времени и размерам уровня должны саг ответствовать равные отрезки масштабной шкалы.

Пример. Рассмотрим построение линейной диаграммы на основании следующих данных:
^ Динамика валового сбора кормовых культур в регионе за 1995-2004 г.

Изображение динамики валового сбора кормовых культур на координатной сетке с неразрывной шкалой значений, начинающихся от нуля, вряд ли целесообразно, так как 2/3 поля диаграммы остается неиспользованным и ничего не дает для выразительности изображения. Поэтому в данных условиях рекомендуется строить шкалу без вертикаль­ного нуля, то есть шкала значений разрывается недалеко от нулевой линии и на диа­грамму попадает лишь часть возможного поля графика. Это не приводит к искажениям в изображении динамики явления и процесс его изменения рисуется диаграммой более четко (рис. 4.13).

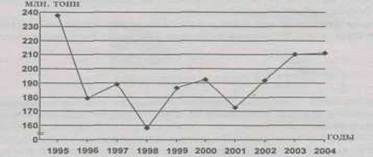
Рис. 4.13. Динамика валового сбора кормовых культур в регионе за 1995-2004 гг.
Нередко на одном линейном графике приводится несколько кривых, которые дают сравнительную характеристику динамики различных показателей или одного и того же показателя в разных странах. Примером графического изображения сразу нескольких по­казателей может служить рис. 4.14.

Линейные диаграммы с равномерной шкалой имеют недостаток, снижающий их познавательную ценность. Этот недостаток заключается в том, что равномерная шкала позволяет измерять и сравнивать только отраженные на диаграмме абсолютные приросты или уменьшения показателей на протяжении исследуемого периода. Однако при изучении динамики важно знать относительные изменения исследуемых показателей по сравнению с достигнутым уровнем или темпы их изменения.

Именно относительные изменения экономических показателей в динамике иска­жаются при изображении их на координатной диаграмме с равномерной вертикальной шкалой. Кроме того, в обычных координатах теряет всякую наглядность и даже становится невозможным изображение рядов динамики с резко изменяющимися уровнями, кото­рые обычно имеют место в динамических рядах за длительный период времени.

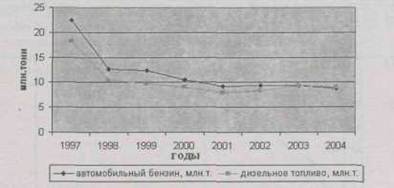
^ Рис. 4.14. Динамика потребления автобензина и дизельного топлива автотранспортом организаций отраслей экономики региона за 1997-2004 гг.
В этих случаях следует отказаться от равномерной шкалы и положить в основу графика полулогарифмическую систему. Полулогарифмической системой называется система, в которой на одной оси нанесен линейный масштаб, а на другой логарифмиче­ский. В данном случае логарифмический масштаб наносится на ось ординат, а на оси абс­цисс располагают равномерную шкалу для отсчета времени по принятым интервалам (го­дам, кварталам, месяцам, дням и прочее). Техника построения логарифмической шкалы следующая: необходимо найти логарифмы исходных чисел; начертить ординату и разде­лить на несколько равных частей. Затем нанести на ординату (или равную ей параллель­ную линию) отрезки, пропорциональные абсолютным приростам этих логарифмов. Далее записать соответствующие логарифмы чисел и их антилогарифмы, например (0,000; 0,3010; 0,4771; 0,6021;...; 1,000, что дает 1, 2, 3, 4..., 10). Полученные антилогарифмы окончательно дают вид искомой шкалы на ординате. Логарифмический масштаб лучше понять на примере.

Пример. Допустим, нужно изобразить на графике динамику производства газа в регионе за 1975-2004 гг., за эти годы его рост составил 9,1 раза. С этой целью находим логарифмы для каждого уровня ряда (см. таблицу 4.1).

^ Таблица 4.1.