Некоторые понятия из теории функций

Определение 1. Множество (комплексных) функций 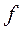, непрерывных вместе со своими производными в области 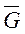, образуют класс функций 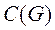, представляющий собой линейное множество:

,

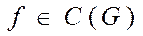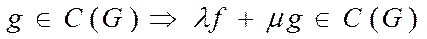
Рассмотрим класс 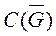непрерывных и ограниченных на замкнутом множестве 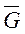функций .

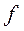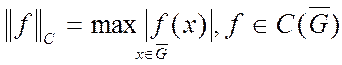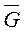( - множество замкнутое, т.е. с границей). Для этого класса можно ввести норму:

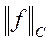-норма для класса функций 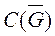. (1)

Определение 2: Линейное пространство 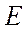называется нормированным, если каждому 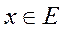поставлено в соответствие неотрицательное число 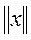(норма x), так что выполняются следующие три аксиомы:

1. 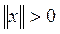; 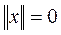в том и только в том случае, когда ;

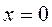2. ;

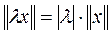3. ;

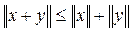Для множества функций:

1. 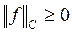; 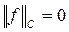в том и только в том случае, когда ;

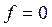2. 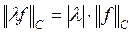, где 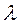- любое комплексное число;

3. 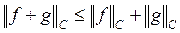-неравенство треугольника;