Определение 3: Линейное нормированное пространство называется полным, если любая принадлежащая ему последовательность 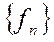 удовлетворяющая условию Коши, сходится к некоторому элементу
удовлетворяющая условию Коши, сходится к некоторому элементу 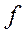 принадлежащему этому пространству.
принадлежащему этому пространству.
Определение 4: Полное линейное нормированное пространство называется банаховым.
Пример банахова пространства пространство 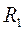 - пространство действительных чисел.
- пространство действительных чисел.
Введем еще одно определение, которое будет использоваться в дальнейшем.
Определение 5: Совокупность всех функций 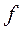 , для которых функция
, для которых функция 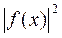 интегрируема на области G обозначается
интегрируема на области G обозначается 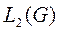 .
.
На этом множестве можно ввести скалярное произведение и норму по формулам:
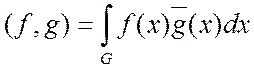 (2)
(2)
( - функция, комплексно сопряженная)
- функция, комплексно сопряженная) 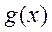
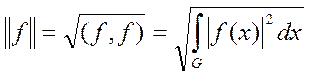 (3)
(3)
Свойства:
1. 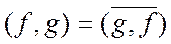 ;
;
2. 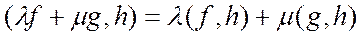 ;
;
Т.о. 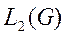 становится линейным нормированным пространством
становится линейным нормированным пространством
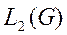 - линейное пространство второго порядка, т.к.
- линейное пространство второго порядка, т.к. 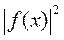 - интегрируемость с квадратом.
- интегрируемость с квадратом.
Определение 6: Функция 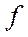 из
из 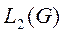 называется нормированной, если
называется нормированной, если 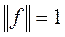 . (4)
. (4)
Определение7: Функция 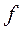 и g из
и g из 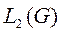 называются ортогональными, если.
называются ортогональными, если. 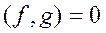 (5)
(5)
Пример:
Система тригонометрических функций: ½, cosx, sinx, cos2x, sin2x, cos3x, sin3x ортогональна на отрезке [0; 2π]: т.е интеграл на отрезке [0; 2π] от произведения двух разных функций этой системы равен 0.
Это вытекает из равенства:
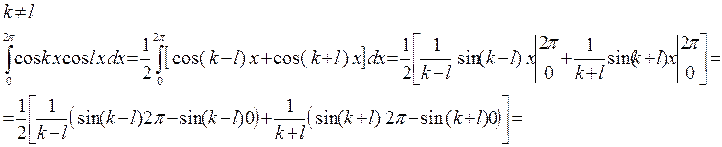
Если k<l, k-l = - p, то sin(- p)=-sin(p), тогда имеем
sin(-2πp)=0 (где р -целое число)
Если k>l, k+l=q то sin2π q =0, (где q -целое число).
Т.е. имеем 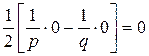
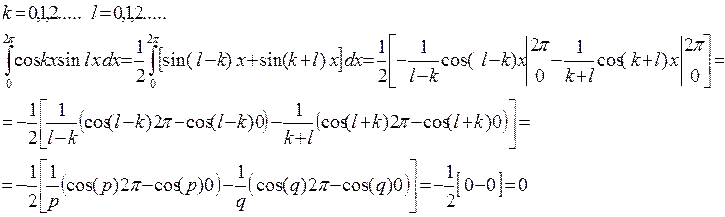
Если l-k>0, l-k=p, l+k=q.
Определение 8: Система функции 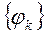 из
из 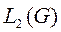 , называется ортонормальной в
, называется ортонормальной в 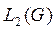 ,если (φk,φi)=σki, где σki-символ Кронекера
,если (φk,φi)=σki, где σki-символ Кронекера

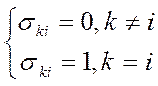 (6)
(6)
Напомним, что всякая ортонормальная система функций 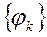 состоит из линейно независимых функций, т.е из того что:
состоит из линейно независимых функций, т.е из того что:
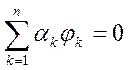 , где αk - числа, откуда следует, что αk=0.
, где αk - числа, откуда следует, что αk=0.
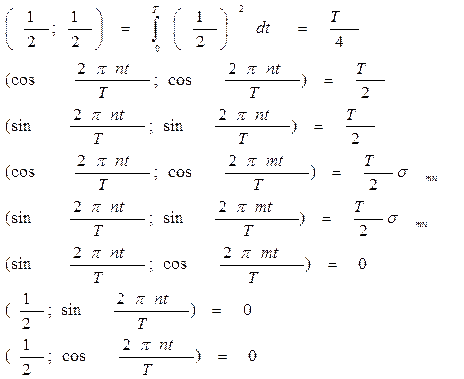
Найдем норму функций для этого тригонометрического ряда:
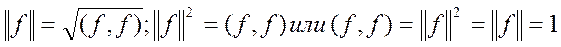 , нормированная система.
, нормированная система.
Рассмотрим более детально:
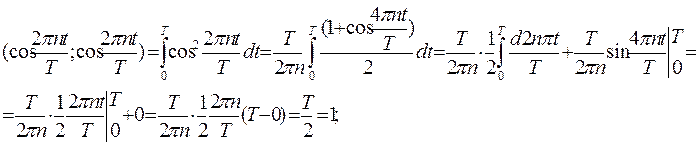
Получили:
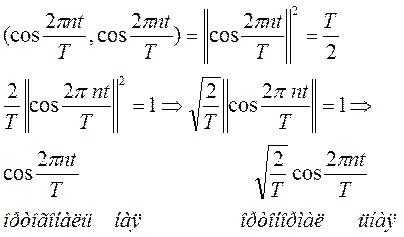
система система
Если Т=2π, то имеем
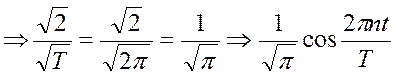
и т.д.
Умножая тригонометрические функции на надлежащие множители можно получить ортонормальную систему.
Примером ортонормальной системы в 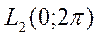 также является следующая тригонометрическая система:
также является следующая тригонометрическая система:
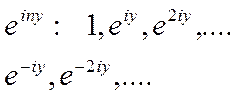 (8)
(8)
(8)- комплексный ряд. Периодичность [0;2π]
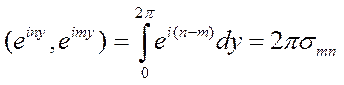
Т.е. система функций ортогональна.
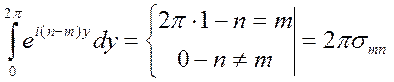
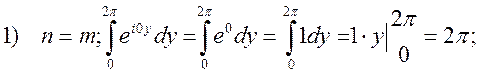
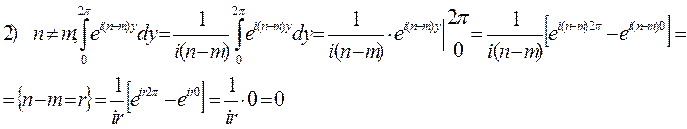
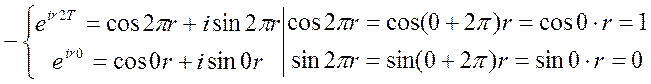
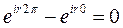
При переходе к ортонормальной системе нормируется на 2π.
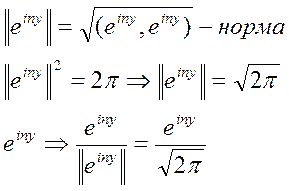
Проверим:
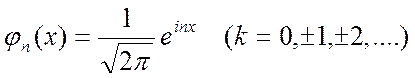
Потому что:
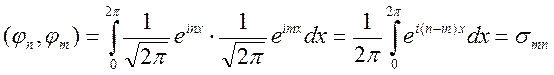
Домашнее задание:
1. Докажите, что система функций: 1,cos x, cos 2x, …,cos nx ортогональна на [0;π].
2. Докажите, что система функций: 1,sin x, sin 2x, …, sin nx ортогональна на [0;π].
Пусть система функций 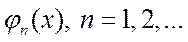 ортогональна в
ортогональна в 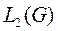 .
.
Наличие ортогональной системы функций позволяет разложить по ней произвольную функцию 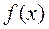 :
:
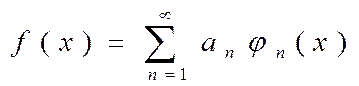 (9)
(9)
Причём области определения 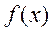 и
и 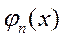 должны быть одинаковы, т.е.
должны быть одинаковы, т.е.
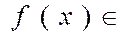
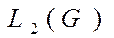 ,
,
или 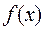 и
и 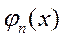 образуют пространство функций
образуют пространство функций 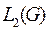 (интегрируемость с квадратом (см. ранее)).
(интегрируемость с квадратом (см. ранее)).
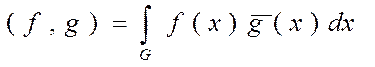
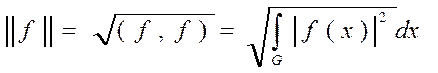
на интервале (a,b)
Для нахождения коэффициентов an, надо
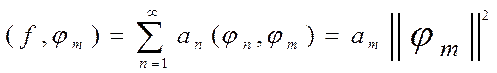 (10)
(10)
(система функций ортогональна и остаётся один член с одинаковыми индексами).
Откуда,
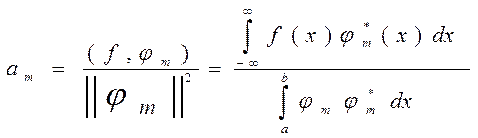 (11)
(11)
Числа 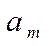 (11) являются коэффициентами ряда Фурье относительно элемента
(11) являются коэффициентами ряда Фурье относительно элемента 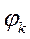 , ортогональной системе
, ортогональной системе 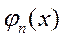 , а ряд (9)
, а ряд (9)
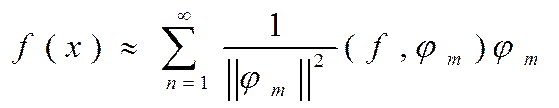 (12)
(12)
является рядом Фурье функции 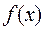 по ортогональной системе
по ортогональной системе 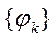 .
. 
 2015-02-27
2015-02-27 683
683








