Этот код содержит постоянное число единиц и нулей. Число кодовых комбинаций составит 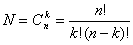
Пример 5.2. Коды с двумя единицами из пяти и тремя единицами из семи.
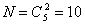
| 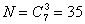
|
Этот код позволяет обнаруживать любые одиночные ошибки и часть многократных ошибок. Не обнаруживаются этим кодом только ошибки смещения, когда одновременно одна единица переходит в ноль и один ноль переходит в единицу, два ноля и две единицы меняются на обратные символы и т.д.
Рассмотрим код с тремя единицами из семи. Для этого кода возможны смещения трех типов.
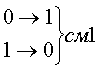
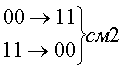
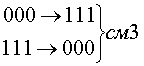
Вероятность появления не обнаруживаемых ошибок смещения
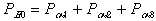 , где
, где 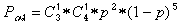
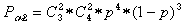
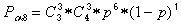
При p<<1 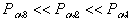 , тогда
, тогда 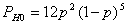
Вероятность появления всевозможных ошибок как обнаруживаемых, так и не обнаруживаемых будет составлять 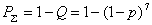
Вероятность обнаруживаемых ошибок 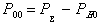 . Тогда коэффициент обнаружения будет равен
. Тогда коэффициент обнаружения будет равен 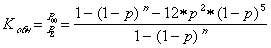
Например, код 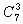 при
при 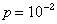 коэффициент обнаружения составит
коэффициент обнаружения составит 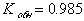 , избыточность L=27%.
, избыточность L=27%.
3. Корреляционный код (Код с удвоением). Элементы данного кода заменяются двумя символами, единица ‘1’ преобразуется в 10, а ноль ‘0’ в 01.
Вместо комбинации 1010011 передается 10011001011010. Ошибка обнаруживается в том случае, если в парных элементах будут одинаковые символы 00 или 11 (вместо 01 и 10).
Например, при k=5, n=10 и вероятности ошибки 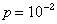 ,
, 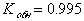 . Но при этом избыточность будет составлять 50%.
. Но при этом избыточность будет составлять 50%.
4. Инверсный код. К исходной комбинации добавляется такая же комбинация по длине. В линию посылается удвоенное число символов. Если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную комбинацию, если нечетное, то добавляемая комбинация является инверсной по отношению к исходной.
| k | r | n |
Прием инверсного кода осуществляется в два этапа. На первом этапе суммируются единицы в первой основной группе символов. Если число единиц четное, то контрольные символы принимаются без изменения, если нечетное, то контрольные символы инвертируются. На втором этапе контрольные символы суммируются с информационными символами по модулю два. Нулевая сумма говорит об отсутствии ошибок. При ненулевой сумме, принятая комбинация бракуется. Покажем суммирование для принятых комбинаций без ошибок (1,3) и с ошибками (2,4).
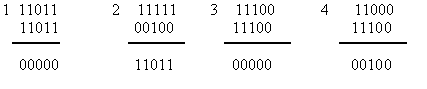
Обнаруживающие способности данного кода достаточно велики. Данный код обнаруживает практически любые ошибки, кроме редких ошибок смещения, которые одновременно происходят как среди информационных символов, так и среди соответствующих контрольных. Например, при k=5, n=10 и 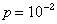 . Коэффициент обнаружения будет составлять
. Коэффициент обнаружения будет составлять 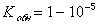 .
.
обнаружения будет составлять 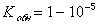 .
.
 2015-02-27
2015-02-27 400
400








