Код Грея записывается следующим образом
| Номер | Код Грея |
| 0 0 0 0 | |
| 0 0 0 1 | |
| 0 0 1 1 | |
| 0 0 1 0 | |
| 0 1 1 0 | |
| 0 1 1 1 | |
| 0 1 0 1 | |
| 0 1 0 0 | |
| 1 1 0 0 | |
| 1 1 0 1 | |
| 1 1 1 1 | |
| 1 1 1 0 | |
| 1 0 1 0 | |
| 1 0 1 1 | |
| 1 0 0 1 | |
| 1 0 0 0 |
Разряды в коде Грея не имеют постоянного веса. Вес k-разряда определяется следующим образом 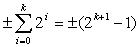 .
.
При этом все нечетные единицы, считая слева направо, имеют положительный вес, а все четные единицы отрицательный.
Например, 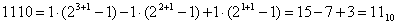
Непостоянство весов разрядов затрудняет выполнение арифметических операций в коде Грея, поэтому необходимо уметь делать перевод кода Грея в обычный двоичный код и наоборот. Алгоритм перевода чисел можно представить следующим образом.
Пусть 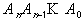 -- двоичный код,
-- двоичный код, 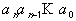 -- код Грея
-- код Грея
Тогда переход из двоичного кода в код Грея выполнится по следующему алгоритму
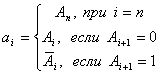
Например, 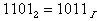 .
.
Обратный переход из кода Грея в двоичный код
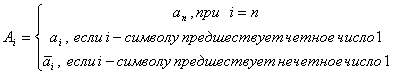

Например, 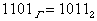 .
.
Рассмотрим невзвешенный двоичный рефлексный код Грея Таблица 2.2
| Десятичное число | Двоичный код вес 8-4-2-1 | Код Грея |
| … | … | … |
Правило получения кода Грея: кодовую комбинацию натурального двоичного кода складывают по модулю 2 с такой же комбинацией, сдвинутой на один разряд вправо, при этом младший разряд сдвинутой комбинации отбрасывается.

Характерные особенности кода Грея:
1) каждая последующая комбинация всегда отличается от предыдущей только в одной позиции (в одном разряде);
2) смена значений элементов в каждом разряде (1 на 0 или 0 на 1) при переходе от комбинации к комбинации в коде Грея происходит вдвое реже, чем в натуральном двоичном коде. Это свойство кода Грея позволяет получить точность кодирования выше по сравнению с натуральным двоичным кодом при том же быстродействии схемы кодирования;
При сложении двух соседних комбинаций кода Грея по модулю 2 (mod2) число единиц равно числу разрядов минус три (n-3). Это свойство кода Грея можно использовать для проверки правильности принятых комбинаций.
В коде Грея можно выделить оси симметрии (оси отражения), относительно которых наблюдается идентичность элементов в некоторых разрядах. Так, например, имеет место симметрия относительно оси, проведенной между числами 7 и 8 (идентичны три символа младших разрядов). Эта особенность и послужила основанием для введения термина «рефлексный», то есть отраженный код.
 2015-02-27
2015-02-27 3935
3935








