Пусть функция f(x,y) определена и непрерывна в ограниченной замкнутой области Д плоскости хОу. Разобьем область Д произвольным образом на n элементарных областей, имеющих площади 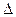 S1 ,
S1 , 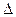 S2,...,
S2,..., 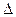 Sn и диаметры d1,d2,..., dn (диаметром называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку Pi(xi, yi) и составим следующую сумму:
Sn и диаметры d1,d2,..., dn (диаметром называется наибольшее из расстояний между двумя точками границы этой области). Выберем в каждой элементарной области произвольную точку Pi(xi, yi) и составим следующую сумму:
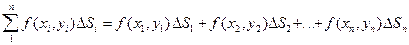 .
.
Такая сумма называется интегральной суммой.
Определение:
Предел интегральной суммы при условии, что число элементарных областей n ® 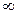 и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит:
и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит:
1) ни от способа разбиения области Д на элементарные области;
2) ни от способа выбора в них точек Рi
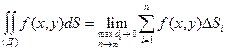 .
.
Если f(x, y) > 0 в области Д, то двойной интеграл 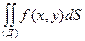 равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).
равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).
Свойства двойного интеграла аналогичны свойствам определенного интеграла.
 2015-02-04
2015-02-04 422
422








