1. Замена переменной в интеграле 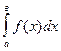 .
.
Делается подстановка х = j(t) и вычисляется дифференциал dx = j¢(t)dt. Находятся новые пределы интегрирования путем решения уравнений а = j(t),
в = j(t) относительно t. Тогда исходный интеграл примет вид:
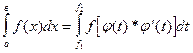 .
.
2. Интегрирование по частям 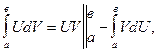
где U = U(x), V = V(x) - непрерывно дифференцируемые функции на [ а, в ].
ЗАДАЧА № 11
Вычислить определенный интеграл:
1. 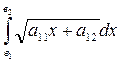 ; 2.
; 2. 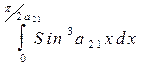 ;
;
3. 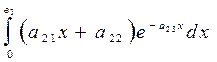 ; 4.
; 4. 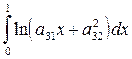 .
.
1. 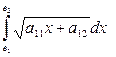 =
= 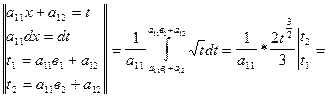
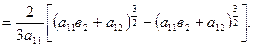
2. 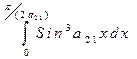 =
= 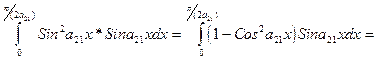
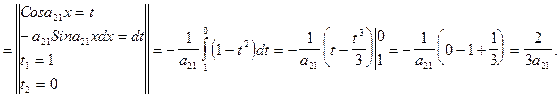
3. 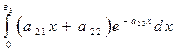 =
= 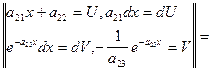
= 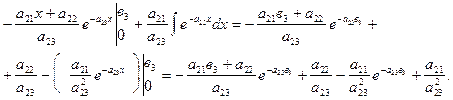
4. 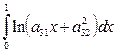 =
= 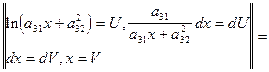
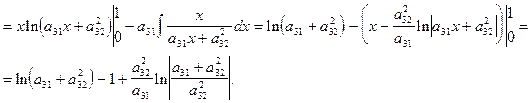
 2015-02-04
2015-02-04 286
286








